题目内容
17.已知$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-2,4),$\overrightarrow{c}$=(-1,-2).(1)求$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$任意两个向量夹角的余弦值;
(2)求$\overrightarrow{a}•\overrightarrow{b}$,($\overrightarrow{a}-\overrightarrow{b}$)•($\overrightarrow{a}+\overrightarrow{b}$),$\overrightarrow{a}•(\overrightarrow{b}+\overrightarrow{c})$,($\overrightarrow{a}+\overrightarrow{b}$)2的值.
分析 (1)根据向量夹角余弦的坐标公式即可求出$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$任意两个向量夹角的余弦值;
(2)根据向量坐标的加法和减法运算可求出向量$\overrightarrow{a}-\overrightarrow{b},\overrightarrow{a}+\overrightarrow{b},\overrightarrow{b}+\overrightarrow{c}$的坐标,然后进行向量数量积的坐标运算即可.
解答 解:(1)$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{8}{\sqrt{13}•2\sqrt{5}}=\frac{4\sqrt{65}}{65}$,$cos<\overrightarrow{a},\overrightarrow{c}>=\frac{\overrightarrow{a}•\overrightarrow{c}}{|\overrightarrow{a}||\overrightarrow{c}|}=\frac{-8}{\sqrt{13}•\sqrt{5}}=-\frac{8\sqrt{65}}{65}$,$cos<\overrightarrow{b},\overrightarrow{c}>=\frac{\overrightarrow{b}•\overrightarrow{c}}{|\overrightarrow{b}||\overrightarrow{c}|}$=$\frac{-6}{2\sqrt{5}•\sqrt{5}}=-\frac{3}{5}$;
(2)$\overrightarrow{a}•\overrightarrow{b}=2×(-2)+3×4=8$,$(\overrightarrow{a}-\overrightarrow{b})•(\overrightarrow{a}+\overrightarrow{b})=(4,-1)•(0,7)=-7$,$\overrightarrow{a}•(\overrightarrow{b}+\overrightarrow{c})=(2,3)•(-3,2)=0$,$(\overrightarrow{a}+\overrightarrow{b})^{2}=(0,7)^{2}=49$.
点评 考查向量夹角余弦的坐标公式,向量数量积的坐标运算,根据向量的坐标求向量的长度,以及向量坐标的加法和减法运算.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案| A. | x+y=0 | B. | x+y=2 | C. | x-y=2 | D. | x-y=-2 |
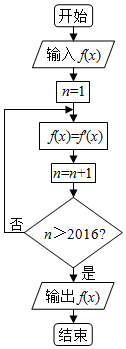 阅读如图所示的程序框图,其中f′(x)是f(x)的导数.已知输入f(x)为sinx,运行相应的程序,输出的结果是( )
阅读如图所示的程序框图,其中f′(x)是f(x)的导数.已知输入f(x)为sinx,运行相应的程序,输出的结果是( )| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |