题目内容
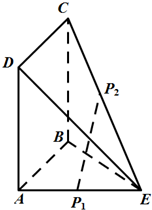 正方形ABCD的边长为1,AE=1,DE=
正方形ABCD的边长为1,AE=1,DE=| 2 |
| 3 |
(Ⅰ)证明:P1P2⊥BD;
(Ⅱ)求四面体P1P2AB体积的最大值.
考点:直线与平面垂直的性质,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)连接AC,DB.AC为平面AEC与平面ABCD的交线,由P1P2∥平面ABCD,推断出P1P2∥AC又平面ABCD为正方形,可知AC⊥BD.进而推断出P1P2⊥BD.
(2))根据CD,DE,CE的值,推断出CD⊥DE.由CD⊥AD,推断出CD⊥平面ADE,进而可知CD⊥AE,AB⊥AE,分别求得BE,CE,判断出CB⊥BE.根据CB⊥BE,CB⊥AB,推断uCB⊥平面ABE.过P2做P2O⊥BE与O点,连接OP1由P2O⊥BE,进而可知P2O⊥平面ABE.连接OP1,可知OP1⊥AE,设AP1=x,则OP1=P1B=1-x,表示出OP2,进而表示出四面体P1P2AB的体积,根据二次函数的性质求得最大值.
(2))根据CD,DE,CE的值,推断出CD⊥DE.由CD⊥AD,推断出CD⊥平面ADE,进而可知CD⊥AE,AB⊥AE,分别求得BE,CE,判断出CB⊥BE.根据CB⊥BE,CB⊥AB,推断uCB⊥平面ABE.过P2做P2O⊥BE与O点,连接OP1由P2O⊥BE,进而可知P2O⊥平面ABE.连接OP1,可知OP1⊥AE,设AP1=x,则OP1=P1B=1-x,表示出OP2,进而表示出四面体P1P2AB的体积,根据二次函数的性质求得最大值.
解答:
证明(1)连接AC,DB.AC为平面AEC与平面ABCD的交线,
∵P1P2∥平面ABCD,
∴P1P2∥AC
又∵平面ABCD为正方形,
∴AC⊥BD.
∴P1P2⊥BD

(2)∵CD=1,DE=
CE=
.
∴CD⊥DE.
∵CD⊥AD,
∴CD⊥平面ADE,
∴CD⊥AE,AB⊥AE,
∵AB⊥AE∴BE=
,
∵BE=
,CE=
,
∴CB⊥BE.
∵CB⊥BE.
CB⊥AB,
∴CB⊥平面ABE.
过P2做P2O⊥BE与O点,连接OP1
∵P2O⊥BE,
∴P2O⊥平面ABE.
连接OP1,
∴OP1⊥AE
设AP1=x,则OP1=P1B=1-x,
△BCE中,
=
=
∴OP2=1-xVP2P1AB1=
×
×AP1×AB×OP2=
x(1-x)当x=
时,最大值为
∵P1P2∥平面ABCD,
∴P1P2∥AC
又∵平面ABCD为正方形,
∴AC⊥BD.
∴P1P2⊥BD

(2)∵CD=1,DE=
| 2, |
| 3 |
∴CD⊥DE.
∵CD⊥AD,
∴CD⊥平面ADE,
∴CD⊥AE,AB⊥AE,
∵AB⊥AE∴BE=
| 2 |
∵BE=
| 2 |
| 3 |
∴CB⊥BE.
∵CB⊥BE.
CB⊥AB,
∴CB⊥平面ABE.
过P2做P2O⊥BE与O点,连接OP1
∵P2O⊥BE,
∴P2O⊥平面ABE.
连接OP1,
∴OP1⊥AE
设AP1=x,则OP1=P1B=1-x,
△BCE中,
| OP2 |
| BC |
| OE |
| BE |
| 1-x |
| 1 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 24 |
点评:本题主要考查线面平行,线面垂直的判定定理,棱锥的体积.考查了学生对立体几何知识综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
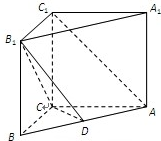 已知直三棱柱ABC-A1B1C1中,AC=BC=AA1=4,AC⊥BC,若D是AB中点.
已知直三棱柱ABC-A1B1C1中,AC=BC=AA1=4,AC⊥BC,若D是AB中点.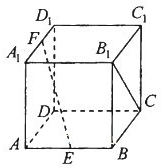 如图,在正方体ABCD-A1B1C1D1中,AB=2,点E、F分别是AB、A1D1的中点.
如图,在正方体ABCD-A1B1C1D1中,AB=2,点E、F分别是AB、A1D1的中点.