题目内容
已知f(x)=|
+
-a|+2a,x∈[0,24],其中a是参数,且a∈[0,
],若把f(x)的最大值记作M(a).
(1)令t=
,x∈[0,24],求t的取值范围;
(2)求函数M(a)解析式;
(3)求函数M(a)值域.
| x |
| x2+1 |
| 1 |
| 3 |
| 3 |
| 4 |
(1)令t=
| x |
| x2+1 |
(2)求函数M(a)解析式;
(3)求函数M(a)值域.
考点:基本不等式,函数的值域
专题:函数的性质及应用,导数的综合应用
分析:(1)利用导数研究函数t(x)的单调性极值与最值即可得出.
(2)令g(t)=|t+
-a|+2a,t∈[0,
].对a分类讨论即可得出;
(3)利用(2)的结论和一次函数的单调性即可得出.
(2)令g(t)=|t+
| 1 |
| 3 |
| 1 |
| 2 |
(3)利用(2)的结论和一次函数的单调性即可得出.
解答:
解:(1)∵t=
,x∈[0,24],
∴t′=
,
令t′=0,解得x=1.
当0<x<1时,t′>0,此时函数t(x)单调递增;当1<x≤1时,t′<0,此时函数t(x)单调递减.
∴当x=1时,函数t(x)取得极大值,即最大值,t(1)=
.
又t(0)=0,t(24)>0,∴t(x)的最小值为0.
∴t∈[0,
].
(2)令g(t)=|t+
-a|+2a,t∈[0,
].
当a-
<
时,即0≤a<
,[g(t)]max=g(
)=|
-a|+2a=a+
.
当a-
≥
时,即
≤a≤
,[g(t)]max=g(0)=|
-a|+2a=3a-
.
∴M(a)=
.
(3)当时a∈[0,
),M(a)∈[
,
);
当a∈[
,
]时,M(a)∈(
,
].
∴M(a)的值域为[
,
].
| x |
| x2+1 |
∴t′=
| -(x+1)(x-1) |
| (x2+1)2 |
令t′=0,解得x=1.
当0<x<1时,t′>0,此时函数t(x)单调递增;当1<x≤1时,t′<0,此时函数t(x)单调递减.
∴当x=1时,函数t(x)取得极大值,即最大值,t(1)=
| 1 |
| 2 |
又t(0)=0,t(24)>0,∴t(x)的最小值为0.
∴t∈[0,
| 1 |
| 2 |
(2)令g(t)=|t+
| 1 |
| 3 |
| 1 |
| 2 |
当a-
| 1 |
| 3 |
| 1 |
| 4 |
| 7 |
| 12 |
| 1 |
| 2 |
| 5 |
| 6 |
| 5 |
| 6 |
当a-
| 1 |
| 3 |
| 1 |
| 4 |
| 7 |
| 12 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
∴M(a)=
|
(3)当时a∈[0,
| 7 |
| 12 |
| 5 |
| 6 |
| 17 |
| 12 |
当a∈[
| 7 |
| 12 |
| 3 |
| 4 |
| 17 |
| 12 |
| 23 |
| 12 |
∴M(a)的值域为[
| 5 |
| 6 |
| 23 |
| 12 |
点评:本题考查了利用导数研究函数t(x)的单调性极值与最值的方法、一次函数的单调性、含绝对值的函数等基础知识与基本技能方法,考查了推理能力和计算能力,考查了分类讨论的思想方法,属于难题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
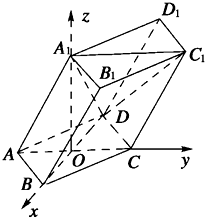 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°. 如图,一艘轮船在某海岛附近的海上匀速直线航行,海岛上一观察哨A在上午11时测得轮船在海岛北偏东60°的B处,12时20分测得轮船在海岛北偏西60°的C处,12时40分轮船到达位于海岛正西方且距离海岛5海里的D港口.
如图,一艘轮船在某海岛附近的海上匀速直线航行,海岛上一观察哨A在上午11时测得轮船在海岛北偏东60°的B处,12时20分测得轮船在海岛北偏西60°的C处,12时40分轮船到达位于海岛正西方且距离海岛5海里的D港口.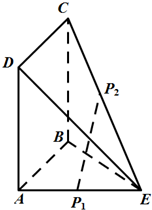 正方形ABCD的边长为1,AE=1,DE=
正方形ABCD的边长为1,AE=1,DE=