题目内容
15.以下三个命题①设回归方程为$\stackrel{∧}{y}$=3-3x,则变量x增加一个单位时,y平均增加3个单位;
②两个随机变量的线性相关性越强,则相关系数的绝对值越接近于1;
③在某项测量中,测量结果ξ服从正态分布N (1,σ2) (σ>0).若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8.
其中真命题的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①,利用一次函数的单调性判定;
②,利用相关性系数r的意义去判断;
③,利用正态分布曲线的性质判.
解答 解:对于①,变量x增加一个单位时,y平均减少3个单位,故错;
对于②,根据线性相关系数r的意义可知,当两个随机变量线性相关性越强,r的绝对值越接近于1,故正确;
对于③,在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0).若ξ在(0,1)内取值的概率为0.4,
则ξ在(0,2)内取值的概率为0.8,符合正态分布的特点,故正确.
故选:C.
点评 本题考查了两个随机变量的线性相关性的性质、正态分布的对称性,考查了推理能力,属中档题

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
3.命题“?x0>0,使得(x0+1)${e}^{{x}_{0}}$>1”的否定是( )
| A. | ?x>0,总有(x+1)ex≤1 | B. | ?x≤0,总有(x+1)ex≤1 | ||
| C. | ?x0≤0,总有(x0+1)${e}^{{x}_{0}}$≤1 | D. | ?x0>0,使得(x0+1)${e}^{{x}_{0}}$≤1 |
20.国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参加抽奖活动的人数越来越多,该分店经理对开业前7天参加抽奖活动的人数进行统计,y表示开业第x天参加抽奖活动的人数,得到统计表格如下:
经过进一步统计分析,发现y与x具有线性相关关系.
(Ⅰ)根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=bx+$\stackrel{∧}{a}$;
(Ⅱ)若该分店此次抽奖活动自开业始,持续10天,参加抽奖的每位顾客抽到一等奖(价值200元奖品)的概率为$\frac{1}{7}$,抽到二等奖(价值100元奖品)的概率为$\frac{2}{7}$,抽到三等奖(价值10元奖品)的概率为$\frac{4}{7}$,试估计该分店在此次抽奖活动结束时送出多少元奖品?
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-n{x}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 5 | 8 | 8 | 10 | 14 | 15 | 17 |
(Ⅰ)根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=bx+$\stackrel{∧}{a}$;
(Ⅱ)若该分店此次抽奖活动自开业始,持续10天,参加抽奖的每位顾客抽到一等奖(价值200元奖品)的概率为$\frac{1}{7}$,抽到二等奖(价值100元奖品)的概率为$\frac{2}{7}$,抽到三等奖(价值10元奖品)的概率为$\frac{4}{7}$,试估计该分店在此次抽奖活动结束时送出多少元奖品?
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-n{x}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$.
4.已知a,b,c分别为△ABC的内角A,B,C所对的边,且3a2+3b2-c2=4ab,则△ABC( )
| A. | 可能为锐角三角形 | B. | 一定不是锐角三角形 | ||
| C. | 一定为钝角三角形 | D. | 不可能为钝角三角形 |
 边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,M为AD上的点,AE=1,AM=$\frac{1}{2}$.
边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,M为AD上的点,AE=1,AM=$\frac{1}{2}$.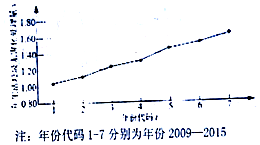 如图是我国2009年至2015年生活垃圾无害化处理量(单位:亿吨)的折线图
如图是我国2009年至2015年生活垃圾无害化处理量(单位:亿吨)的折线图