题目内容
5. 边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,M为AD上的点,AE=1,AM=$\frac{1}{2}$.
边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,M为AD上的点,AE=1,AM=$\frac{1}{2}$.(Ⅰ)求证:EM⊥BD;
(Ⅱ)设点F是棱BC上一点,若二面角A-DE-F的余弦值为$\frac{\sqrt{10}}{10}$,试确定点F在BC上的位置.
分析 (Ⅰ)由AE⊥平面CDE,可得AE⊥DE,AE⊥CD,由已知可得AD⊥CD,利用线面垂直的判定可得CD⊥平面ADE,得到CD⊥ME,求解△AME中可得ME⊥AM.从而得到ME⊥平面ABCD,即ME⊥BD;
(Ⅱ)由(Ⅰ)知,CD⊥DE,建立空间直角坐标系D-xyz,可得D,C,E,A的坐标,求出所用向量的坐标,求得平面FDE与平面ADE的法向量,利用两法向量所成角的余弦值列式求解点F在BC上的位置.
解答 (Ⅰ)证明:∵AE⊥平面CDE,∴AE⊥DE,AE⊥CD,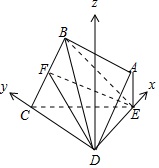
∵AD⊥CD,∴CD⊥平面ADE,则CD⊥ME,
∵AD=2,AE=1,∴∠DAE=60°,
在△AME中,AE=1,AM=$\frac{1}{2}$,由余弦定理可得:ME=$\frac{\sqrt{3}}{2}$.
∴AE2=AM2+ME2,则ME⊥AM.
∴ME⊥平面ABCD,
∴ME⊥BD;
(Ⅱ)解:由(Ⅰ)知,CD⊥DE,建立如图所示空间直角坐标系D-xyz,
则D(0,0,0),C(0,2,0),E($\sqrt{3},0,0$),A($\sqrt{3},0,1$),
∴$\overrightarrow{AB}=\overrightarrow{DC}=(0,2,0)$,$\overrightarrow{DB}=\overrightarrow{DA}+\overrightarrow{AB}$,则B($\sqrt{3},2,1$).
设$\overrightarrow{CF}=λ\overrightarrow{CB}=λ(\sqrt{3},0,1)$,λ∈[0,1],则F($\sqrt{3}λ,2,λ$),
设平面FDE的法向量$\overrightarrow{n}=(x,y,z)$,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DF}=\sqrt{3}λx+2y+λz=0}\\{\overrightarrow{n}•\overrightarrow{DE}=\sqrt{3}x=0}\end{array}\right.$,取z=-2,则$\overrightarrow{n}=(0,λ,-2)$,
又平面ADE的法向量为$\overrightarrow{m}=(0,1,0)$,
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}=\frac{λ}{\sqrt{{λ}^{2}+4}}=\frac{\sqrt{10}}{10}$,解得$λ=\frac{2}{3}$.
故当点F满足$\overrightarrow{CF}=\frac{2}{3}\overrightarrow{CB}$时,二面角A-DE-F的余弦值为$\frac{\sqrt{10}}{10}$.
点评 本题考查空间中直线与直线的位置关系,考查空间想象能力和思维能力,训练了利用等积法求二面角的平面角,是中档题.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案| A. | aial≤ajak | B. | aial≥ajak | C. | SiSl<SjSk | D. | SiSl≥SjSk |
| A. | 向左平移$\frac{π}{12}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
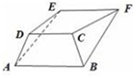 我国古代数学名著《九章算术》中有:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?”羡除即三个面是等腰梯形、两侧面是三角形的五面梯形ABCDEF隧道(如图),其中,等腰梯形ABCD的下、上底边长分别为6尺和1丈,高为3尺,平面ABCD⊥平面ABFE,等腰梯形ABFE的上底边长为8尺,高为7尺,则得到此“羡除”的容积( )
我国古代数学名著《九章算术》中有:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?”羡除即三个面是等腰梯形、两侧面是三角形的五面梯形ABCDEF隧道(如图),其中,等腰梯形ABCD的下、上底边长分别为6尺和1丈,高为3尺,平面ABCD⊥平面ABFE,等腰梯形ABFE的上底边长为8尺,高为7尺,则得到此“羡除”的容积( )| A. | 约84立方尺 | B. | 约为105立方尺 | C. | 恰为84立方尺 | D. | 恰为105立方尺 |
| A. | $λ<\frac{4}{5}$ | B. | λ<1 | C. | $λ<\frac{3}{2}$ | D. | $λ<\frac{2}{3}$ |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |