题目内容
7.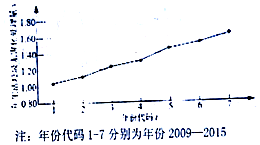 如图是我国2009年至2015年生活垃圾无害化处理量(单位:亿吨)的折线图
如图是我国2009年至2015年生活垃圾无害化处理量(单位:亿吨)的折线图(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2017年我国生活垃圾无害化处理量.
参考数据:$\sum_{i=1}^{7}$yi=9.32,$\sum_{i=1}^{7}$tiyi=40.17,$\sqrt{{\sum_{i=1}^{7}{(y}_{i}-\overline{y})}^{2}}$=0.55,$\sqrt{7}$≈2.646.
参考公式:相关系数r=$\frac{\sum_{i=1}^{n}{(t}_{i}-\overline{t}){(y}_{i}-\overline{y})}{\sqrt{{\sum_{i=1}^{n}{(t}_{i}-\overline{t})}^{2}{\sum_{i=1}^{n}{(y}_{i}-\overline{y})}^{2}}}$=$\frac{n{{\sum_{i=1}^{n}t}_{i}y}_{i}-{\sum_{i=1}^{n}t}_{i}•{\sum_{i=1}^{n}y}_{i}}{n\sqrt{{\sum_{i=1}^{n}{(t}_{i}-\overline{t})}^{2}{\sum_{i=1}^{n}{(y}_{i}-\overline{y})}^{2}}}$
回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{a}$+$\stackrel{∧}{b}$t中斜率和截距的最小二乘估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{(t}_{i}-\overline{t}){(y}_{i}-\overline{y})}{{\sum_{i=1}^{n}{(t}_{i}-\overline{t})}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$t.
分析 (1)求出变量y与t的相关系数,可得结论;
(2)求出回归系数,可得回归方程,即可预测2017年我国生活垃圾无害化处理1.83亿吨.
解答 解:(1)变量y与t的相关系数r=$\frac{7×40.17-28×9.32}{7×5.292×0.55}$≈0.99,….(5分)
故可用线性回归模型拟合变量y与t的关系.…..(6分)
(2)$\overline{t}$=4,$\overline{y}$=$\frac{1}{7}$$\sum_{i=1}^{7}$yi,所以$\stackrel{∧}{b}$=$\frac{40.17-7×4×\frac{1}{7}×9.32}{28}$=0.1,
$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$t=$\frac{1}{7}×9.32-0.10×4≈0.93$,…..(10分)
所以线性回归方程为$\stackrel{∧}{y}$=0.1t+0.93,
当t=9时,$\stackrel{∧}{y}$=0.1×9+0.93=1.83,
因此,我们可以预测2017年我国生活垃圾无害化处理1.83亿吨 …(12分)
点评 本题考查回归方程,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
17.已知圆O:x2+y2=1交x轴正半轴于点A,在圆O上随机取一点B,则使$|{\overrightarrow{OA}-\overrightarrow{OB}}|≤1$成立的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
18.集合A={x|3x+2>0},B={x|$\frac{x+1}{x-3}$<0},则A∩B=( )
| A. | (-1,+∞) | B. | (-1,-$\frac{2}{3}$) | C. | (3,+∞) | D. | (-$\frac{2}{3}$,3) |
2.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名六年级学生进行了问卷调查得到如图联表.且平均每天喝500ml以上为常喝,体重超过50kg为肥胖.已知在全部100人中随机抽取1人,抽到肥胖的学生的概率为0.8.
(1)求肥胖学生的人数并将上面的列联表补充完整;
(2)是否有95%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
附:参考公式:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 60 | ||
| 不肥胖 | 10 | ||
| 合计 | 100 |
(2)是否有95%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
附:参考公式:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$
| P(x2≥x0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
19.已知等差数列{an}中,a1+a4+a7=$\frac{5}{4}π$,那么cos(a3+a5)=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
16.两列火车从同一站台沿相反方向开去,走了相同的路程,设两列火车的位移向量分别为$\overrightarrow{a}$和$\overrightarrow{b}$,则下列说法中错误的是( )
| A. | $\overrightarrow{a}$与$\overrightarrow{b}$为平行向量 | B. | $\overrightarrow{a}$与$\overrightarrow{b}$为模相等的向量 | ||
| C. | $\overrightarrow{a}$与$\overrightarrow{b}$为共线向量 | D. | $\overrightarrow{a}$与$\overrightarrow{b}$为相等的向量 |