题目内容
7.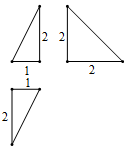 已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )
已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 由三视图还原原几何体,补形找出异面直线所成角,求解三角形得答案.
解答 解:由三视图还原原几何体如图:
几何体是三棱锥A-BCD,满足面ACD⊥面BCD,且AD⊥CD,BC⊥CD.
最短棱为CD,最长棱为AB.
在平面BCD内,过B作BE∥CD,且BE=CD,
∴四边形BEDC为正方形,可得AE=2$\sqrt{2}$,
在Rt△AEB中,求得AB=$\sqrt{{1}^{2}+(2\sqrt{2})^{2}}=3$,
∴cos∠ABE=$\frac{BE}{AB}=\frac{1}{3}$.
即最短的棱和最长的棱所在直线的成角余弦值为$\frac{1}{3}$.
故选:A.
点评 本题考查空间几何体的三视图,考查异面直线所成角的求法,是中档题.

练习册系列答案
相关题目
17.已知集合M={x|x(4-x)<0},N={x|(x-1)(x-6)<0,x∈Z},则M∩N=( )
| A. | (1,6) | B. | (4,6) | C. | {4,5,6} | D. | {5} |
15.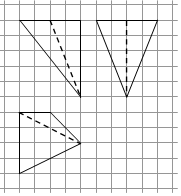 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该几何体的体积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该几何体的体积为( )| A. | 15 | B. | 16 | C. | $\frac{50}{3}$ | D. | $\frac{53}{3}$ |
17.某设备的使用年数x与所支出的维修总费用y的统计数据如下表:
根据上表可得回归直线方程为$\widehat{y}$=1.3x+$\widehat{a}$.若该设备维修总费用超过12万元就报废,据此模型预测该设备最多可使用10年.
| 使用年数x(单位:米) | 2 | 3 | 4 | 5 | 6 |
| 维修总费用y(单位:万元) | 1.5 | 4.5 | 5.5 | 6.5 | 7.5 |
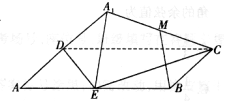 如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中:
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中: