题目内容
15.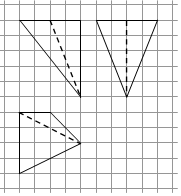 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该几何体的体积为( )| A. | 15 | B. | 16 | C. | $\frac{50}{3}$ | D. | $\frac{53}{3}$ |
分析 由已知中的三视图,可知该几何体是一个以四边形为底面的四棱锥,其高为5,求出底面面积,代入棱锥体积公式,可得几何体的体积.
解答 解:由已知中的三视图,可知该几何体是一个以四边形为底面的四棱锥,其高为5.
底面面积S=梯形+三角形组成.
S梯形=$\frac{1}{2}$(4+3)×2=7;
S三角形=$\frac{1}{2}$×3×2=3.
∴底面面积S=10.
该几何体的体积$V=\frac{1}{3}×10×5=\frac{50}{3}$.
故选C.
点评 本题考查的知识点是由三视图求体积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
5.用反证法证明命题“设a,b为实数,则方程x2+ax+b=0没有实数根”时,要做的假设是( )
| A. | 方程x2+ax+b=0至多有一个实根 | B. | 方程x2+ax+b=0至少有一个实根 | ||
| C. | 方程x2+ax+b=0至多有两个实根 | D. | 方程x2+ax+b=0恰好有两个实根 |
3.复数$\frac{3+4i}{{{{(1-i)}^2}}}$=( )
| A. | $-2+\frac{3}{2}i$ | B. | $-2-\frac{3}{2}i$ | C. | $2+\frac{3}{2}i$ | D. | $2-\frac{3}{2}i$ |
10.已知$sinα+cosα=\frac{1}{5}$,且$-\frac{π}{2}≤α≤\frac{π}{2}$,那么tanα等于( )
| A. | $-\frac{4}{3}$ | B. | $-\frac{3}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
7.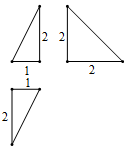 已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )
已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )
 已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )
已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
4.若函数f(x)=a3-cosx,则f'(a)=( )
| A. | 3a2+sina | B. | 3a2-sina | C. | sina | D. | cosa |
5. 把一个皮球放入如图所示的由8根长均为20cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都相切,则皮球的半径为( )
把一个皮球放入如图所示的由8根长均为20cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都相切,则皮球的半径为( )
 把一个皮球放入如图所示的由8根长均为20cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都相切,则皮球的半径为( )
把一个皮球放入如图所示的由8根长均为20cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都相切,则皮球的半径为( )| A. | l0$\sqrt{3}$cm | B. | 10 cm | C. | 10$\sqrt{2}$cm | D. | 30cm |