题目内容
6.已知函数$f(x)=\frac{a}{x}-1+lnx$,若存在x0>0,使得f(x0)≤0有解,则实数a的取值范围是( )| A. | (2,+∞) | B. | (-∞,3) | C. | (-∞,1] | D. | [3,+∞) |
分析 利用参数分离法进行转化,构造函数求出函数的单调性和极值即可得到结论.
解答 解:若存在x0>0,使得f(x0)≤0有解,
则由f(x)=$\frac{a}{x}$-1+lnx≤0,即$\frac{a}{x}$≤1-lnx,
即a≤x-xlnx,设h(x)=x-xlnx,
则h′(x)=1-(lnx+x•$\frac{1}{x}$)=1-lnx-1=-lnx,
由h′(x)>0得-lnx>0,即lnx<0,得0<x<1,此时函数递增,
由h′(x)<0得-lnx<0,即lnx>0,得x>1,此时函数递减,
即当x=1时,函数h(x)取得极大值h(1)=1-ln1=1,
即h(x)≤1
若a≤x-xlnx,有解,则a≤1,
故选:C.
点评 本题主要考查根的存在性性问题,利用参数分离法,构造函数求出函数的极值,注意本题是存在性问题,不是恒成立问题,注意两者的区别.

练习册系列答案
相关题目
1.若f(x)=-$\frac{1}{2}$(x-2)2+blnx在(1,+∞)上是减函数,则b的取值范围是( )
| A. | [-1,+∞) | B. | (-1,+∞) | C. | (-∞,-1] | D. | (-∞,-1) |
11.直线l:y=k(x-2)与双曲线C:x2-y2=2的左右两支各有一个交点,则k的取值范围为( )
| A. | k≤-1或k≥1 | B. | -1≤k≤1 | C. | -$\sqrt{2}$<k<$\sqrt{2}$ | D. | -1<k<1 |
4.设a,b是异面直线,a?平面α,则过直线b与平面α平行的平面( )
| A. | 不存在 | B. | 一定有1个 | C. | 至多有1个 | D. | 一定有2个以上 |
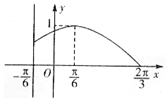 已知定义在区间[-π,$\frac{2}{3}$π]上的函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}<φ<\frac{π}{2}$)的图象关于直线x=-$\frac{π}{6}$对称,当x∈$[-\frac{π}{6},\frac{2π}{3}]$时,f(x)的图象如图所示.
已知定义在区间[-π,$\frac{2}{3}$π]上的函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}<φ<\frac{π}{2}$)的图象关于直线x=-$\frac{π}{6}$对称,当x∈$[-\frac{π}{6},\frac{2π}{3}]$时,f(x)的图象如图所示.