题目内容
16.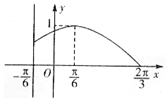 已知定义在区间[-π,$\frac{2}{3}$π]上的函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}<φ<\frac{π}{2}$)的图象关于直线x=-$\frac{π}{6}$对称,当x∈$[-\frac{π}{6},\frac{2π}{3}]$时,f(x)的图象如图所示.
已知定义在区间[-π,$\frac{2}{3}$π]上的函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}<φ<\frac{π}{2}$)的图象关于直线x=-$\frac{π}{6}$对称,当x∈$[-\frac{π}{6},\frac{2π}{3}]$时,f(x)的图象如图所示.(1)求f(x)在$[-π,\frac{2}{3}π]$上的表达式;
(2)求方程f(x)=$\frac{{\sqrt{2}}}{2}$的解.
分析 (1)由函数的图象求出A、T和ω、φ的值,写出函数的解析式;
(2)由解析式可得函数在区间[-$\frac{π}{6}$,$\frac{2π}{3}$]的解,再结合对称性得出函数在对称区间内的解.
解答 解:(1)由图知:A=1,T=4($\frac{2π}{3}$-$\frac{π}{6}$)=2π,
∴ω=$\frac{2π}{T}$=1,
当x∈[-$\frac{π}{6}$,$\frac{2π}{3}$]时,将($\frac{π}{6}$,1)代入f(x)得
f($\frac{π}{6}$)=sin($\frac{π}{6}$+φ)=1,
又0<φ≤π,
∴φ=$\frac{π}{3}$,
∴当x∈[-$\frac{π}{6}$,$\frac{2π}{3}$]时,f(x)=sin(x+$\frac{π}{3}$);
同理可得当x∈[-π,-$\frac{π}{6}$]时,f(x)=sin(x+π)=-sinx;
综上,f(x)=$\left\{\begin{array}{l}{sin(x+\frac{π}{3}),x∈[-\frac{π}{6},\frac{2π}{3}]}\\{-sinx,x∈[-π,-\frac{π}{6})}\end{array}\right.$;
(2)由f(x)=$\frac{\sqrt{2}}{2}$,当x∈[-$\frac{π}{6}$,$\frac{2π}{3}$]时,sin(x+$\frac{π}{3}$)=$\frac{\sqrt{2}}{2}$,
解得x1=$\frac{5π}{12}$,x2=-$\frac{π}{12}$,
∵y=f(x)图象关于直线x=-$\frac{π}{6}$对称,
∴x3=2×(-$\frac{π}{6}$)-(-$\frac{π}{12}$)=-$\frac{π}{4}$,
x4=2×(-$\frac{π}{6}$)-$\frac{5π}{12}$=-$\frac{3π}{4}$,
综上,方程f(x)=$\frac{\sqrt{2}}{2}$的解为:$\frac{5π}{12}$,-$\frac{π}{12}$,-$\frac{π}{4}$,-$\frac{3π}{4}$.
点评 本题考查了三角函数解析式的确定以及分类讨论思想和函数图象的对称性问题,是中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 12 | B. | 15 | C. | 18 | D. | 24 |
| A. | 32 | B. | 64 | C. | $16\sqrt{7}$ | D. | $16\sqrt{3}$ |
| A. | (2,+∞) | B. | (-∞,3) | C. | (-∞,1] | D. | [3,+∞) |