题目内容
用反证法证明命题“已知A，B，C，D是空间中的四点，直线AB与CD是异面直线，则直线AC和BD也是异面直线．”应假设（ ）
| A、直线AC和BD是平行直线 |
| B、直线AB和CD是平行直线 |
| C、直线AC和BD是共面直线 |
| D、直线AB和CD是共面直线 |
考点：反证法与放缩法
专题：证明题,反证法
分析：用反证法证明命题时，应假设命题的否定成立
解答：
解：用反证法证明命题：“若直线AB、CD是异面直线，
则直线AC、BD也是异面直线”应假设直线AC、BD是共面直线，
故选：C．
则直线AC、BD也是异面直线”应假设直线AC、BD是共面直线，
故选：C．
点评：本题主要考查求一个命题的否定，用反证法证明数学命题，把要证的结论进行否定，得到要证的结论的否定，是解题的突破口．
练习册系列答案
相关题目
已知向量
=（-1，2），
=（x，4），且
∥
，则x的值为（ ）
| a |
| b |
| a |
| b |
| A、8 | B、2 | C、-2 | D、-8 |
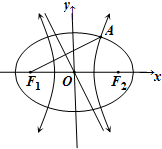如图，F1，F2是椭圆C1：| x2 |
| m2 |
| y2 |
| n2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 | ||
|
| 1 | ||
|
| A、2 | ||
B、
| ||
C、
| ||
| D、4 |
双曲线2x2-y2=8的虚轴长是（ ）
| A、2 | ||
B、2
| ||
| C、4 | ||
D、4
|
由0，1，2，3这四个数字可以组成没有重复数字且不能被5整除的四位数的个数是（ ）
| A、24个 | B、12个 |
| C、6个 | D、4个 |
已知定义在（0，π）的函数 f（x）=sinx-
x，则f（x）的单调递减区间为（ ）
| 1 |
| 2 |
| A、（0，π） | ||
B、（0，
| ||
C、（
| ||
D、（
|
已知p：∅⊆{0}；q：{1}∈{1，2}．由它们构成的以下三个命题中，真命题有（ ）
①p∧q ②p∨q ③￢p．
①p∧q ②p∨q ③￢p．
| A、1个 | B、2个 | C、3个 | D、0个 |