题目内容
已知AB、MN为圆C:(x-2)2+y2=9的两条相互垂直的弦,垂足为R(3,a),若四边形ABMN的面积的最大值为14,则a= .
考点:直线与圆的位置关系
专题:直线与圆
分析:如图所示,①当AB或MN中有一条为直径而另一条垂直于x轴时,不妨设此时|AB|=6,|MN|=2
=2
,可得四边形ABMN的面积,判定是否符合条件;
②当AB,MN都不为直径时,分别过圆心作到两条垂直弦的垂线,设到弦的距离分别d1,d2.可得
+
=(3-2)2+a2=1+a2.
假设存在a的值满足条件,则
|AB| |MN|=14,可得|AB||MN|=28.利用垂径定理和勾股定理可得:(
|AB|)2=9-
,(
|MN|)2=9-
,再利用基本不等式的性质可得|AB|2+|MN|2=72-4(
+
)=68-4a2≥2|AB||MN|=56,化为a2≤2,即可得出a的值.
| r2-(3-2)2 |
| 2 |
②当AB,MN都不为直径时,分别过圆心作到两条垂直弦的垂线,设到弦的距离分别d1,d2.可得
| d | 2 1 |
| d | 2 2 |
假设存在a的值满足条件,则
| 1 |
| 2 |
| 1 |
| 2 |
| d | 2 1 |
| 1 |
| 2 |
| d | 2 2 |
| d | 2 1 |
| d | 2 2 |
解答:
解:如图所示,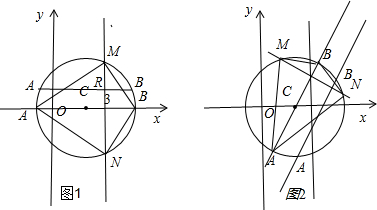 ①当AB或MN中有一条为直径而另一条垂直于x轴时,不妨设此时|AB|=6,|MN|=2
①当AB或MN中有一条为直径而另一条垂直于x轴时,不妨设此时|AB|=6,|MN|=2
=2
,可得SANBM=
×6×4
=12
>14,不符合条件,应舍去;
②当AB,MN都不为直径时,分别过圆心作到两条垂直弦的垂线,设到弦的距离分别d1,d2.
则
+
=(3-2)2+a2=1+a2.
假设存在a的值满足条件,则
|AB| |MN|=14,
可得|AB||MN|=28.
利用垂径定理和勾股定理可得:(
|AB|)2=9-
,(
|MN|)2=9-
,
∴|AB|2+|MN|2=72-4(
+
)=68-4a2≥2|AB||MN|=56,化为a2≤3,
当且仅当a=±
时取等号,此时|AB|=|MN|.
故答案为:±
.
 ①当AB或MN中有一条为直径而另一条垂直于x轴时,不妨设此时|AB|=6,|MN|=2
①当AB或MN中有一条为直径而另一条垂直于x轴时,不妨设此时|AB|=6,|MN|=2| r2-(3-2)2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
②当AB,MN都不为直径时,分别过圆心作到两条垂直弦的垂线,设到弦的距离分别d1,d2.
则
| d | 2 1 |
| d | 2 2 |
假设存在a的值满足条件,则
| 1 |
| 2 |
可得|AB||MN|=28.
利用垂径定理和勾股定理可得:(
| 1 |
| 2 |
| d | 2 1 |
| 1 |
| 2 |
| d | 2 2 |
∴|AB|2+|MN|2=72-4(
| d | 2 1 |
| d | 2 2 |
当且仅当a=±
| 3 |
故答案为:±
| 3 |
点评:熟练掌握垂径定理、圆的标准方程、勾股定理、两点间的公式、分类讨论思想方法等是解题的关键.

练习册系列答案
相关题目
不等式
的解集是( )
|
| A、{x|x<1} |
| B、{x|x>-4} |
| C、{x|-4<x<1} |
| D、{x|x>1} |
若函数f(x)=asinx-bcosx在x=
处有最小值-2,则常数a、b的值是( )
| π |
| 3 |
A、a=-1,b=
| ||
B、a=1,b=-
| ||
C、a=
| ||
D、a=-
|
在△ABC中,a=2,A=30°,C=120°,则△ABC的面积为( )
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|