题目内容
已知正项数列{an}中,a1=2,点(
,an+1)在函数y=x2+1的图象上,数列{bn}中,点(bn,Tn)在直线y=-
x+3上,其中Tn是数列{bn}的前n项和(n∈N*).
(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Tn.
| an |
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Tn.
考点:数列与解析几何的综合,数列的求和
专题:综合题,等差数列与等比数列
分析:(1)由点(
,an+1)在函数y=x2+1的图象上,可得an+1=an+1,从而可知{an}为公差为1的等差数列,由等差数列的通项公式可得答案;
(2)由点(bn,Tn)在直线y=-
x+3上,得Tn=-
bn+3①,从而可得Tn+1=-
bn+1+3②,两式作差可得数列递推式,据此可判断该数列为等比数列,由等比数列通项公式可得答案;
| an |
(2)由点(bn,Tn)在直线y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)因为点(
,an+1)在函数y=x2+1的图象上,
所以an+1=an+1,故{an}为公差为1的等差数列,
又a1=2,所以an=2+(n-1)•1=n+1.
(2)因为点(bn,Tn)在直线y=-
x+3上,
所以Tn=-
bn+3①,
则Tn+1=-
bn+1+3②,
②-①得,bn+1=-
bn+1+
bn,即bn+1=
bn,
由T1=-
b1+3得b1=2,
所以{bn}是以
为公比的等比数列,
所以bn=2•(
)n-1.
| an |
所以an+1=an+1,故{an}为公差为1的等差数列,
又a1=2,所以an=2+(n-1)•1=n+1.
(2)因为点(bn,Tn)在直线y=-
| 1 |
| 2 |
所以Tn=-
| 1 |
| 2 |
则Tn+1=-
| 1 |
| 2 |
②-①得,bn+1=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
由T1=-
| 1 |
| 2 |
所以{bn}是以
| 1 |
| 3 |
所以bn=2•(
| 1 |
| 3 |
点评:本题考查数列与解析几何的综合、等差数列等比数列概念,考查学生分析解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
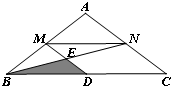 如图所示,在△ABC中,AB=AC=10cm,BC=16cm,M、N、D分别是AB、AC、BC的中点,连接DM、BN交于点E,则图中阴影部分△BDE的面积为( )
如图所示,在△ABC中,AB=AC=10cm,BC=16cm,M、N、D分别是AB、AC、BC的中点,连接DM、BN交于点E,则图中阴影部分△BDE的面积为( )| A、4cm2 |
| B、6cm2 |
| C、8cm2 |
| D、12cm2 |
