题目内容
已知集合A={x|0＜3-x≤4}，集合B={x|2x≥log381}，求A∩B．
考点：其他不等式的解法,交集及其运算
专题：计算题
分析：直接求解集合A，通过解指数不等式求出集合B，然后求解交集．
解答：
解：由0＜3-x≤4⇒-1≤x＜3∴A=[-1，3）
由2x≥log381⇒x≥2∴B=[2，+∞）
∴A∩B=[2，3）．
由2x≥log381⇒x≥2∴B=[2，+∞）
∴A∩B=[2，3）．
点评：本题考查指数不等式的解法，集合交集的求法，基本知识的考查．
练习册系列答案
相关题目
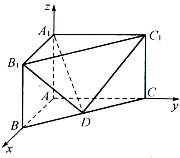三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中．已知AB=2，AC=4，A1A=3，D是BC的中点．（1）求直线DB1与平面A1C1D所成角的正弦值；
（2）求二面角B1-A1D-C1的正弦值．
已知a＞b＞c，下列不等式成立的是（ ）
| A、-a＞-b | ||||
| B、a+c＜b+c | ||||
| C、2a＞2b | ||||
D、
|
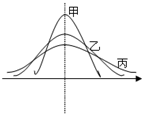某次市教学质量检测，甲、乙、丙三科考试成绩的直方图如图所示（由于人数众多，成绩分布的直方图可视为正态分布），则由图中曲线可得下列说法中正确的一个是（ ）| A、甲科总体的标准差最小 |
| B、乙科总体的标准差及平均数都居中 |
| C、丙科总体的平均数最小 |
| D、甲、乙、丙的总体的平均数不相同 |