题目内容
已知α、β∈(0,
),且sinα=
,cosβ=
,
(1)求cos(α-β)
(2)求α-β
| π |
| 2 |
| ||
| 5 |
| ||
| 10 |
(1)求cos(α-β)
(2)求α-β
考点:两角和与差的余弦函数,同角三角函数间的基本关系
专题:三角函数的求值
分析:(1)根据同角三角函数的基本关系求出cosα和sinβ的值,然后由两角和与差的余弦函数公式并将相应的值代入即可.
(2)根据角的范围得出α-β∈(-
,
),由(1)知cos(α-β)=
即可得出结果.
(2)根据角的范围得出α-β∈(-
| π |
| 2 |
| π |
| 2 |
| ||
| 2 |
解答:
解:(1)∵sinα=
,cosβ=
,α、β∈(0,
),
∴cosα=
=
sinβ=
2=
∴cos(α-β)=cosαcosβ+sinαsinβ=
×
+
×
=
(2)∵α,β∈(0,
),
∴-β∈(-
,0)
∴α-β∈(-
,
)
∵cos(α-β)=
∴α-β=
或-
| ||
| 5 |
| ||
| 10 |
| π |
| 2 |
∴cosα=
1-(
|
2
| ||
| 5 |
1-(
|
3
| ||
| 10 |
∴cos(α-β)=cosαcosβ+sinαsinβ=
2
| ||
| 5 |
| ||
| 10 |
| ||
| 5 |
3
| ||
| 10 |
| ||
| 2 |
(2)∵α,β∈(0,
| π |
| 2 |
∴-β∈(-
| π |
| 2 |
∴α-β∈(-
| π |
| 2 |
| π |
| 2 |
∵cos(α-β)=
| ||
| 2 |
∴α-β=
| π |
| 4 |
| π |
| 4 |
点评:此题考查了同角三角函数的基本关系、两角和与差的余弦函数公式以及特殊角的三角函数值,熟记公式是解题的关键,属于基础题.

练习册系列答案
相关题目
记R为实数集,P为所有平面向量的集合,设a,b,c∈R,
,
,
∈P.则下列类比所得的结论正确的是( )
| x |
| y |
| z |
A、由a•b∈R,类比得
| ||||||||||||
B、由(ab)c=(bc)a,类比得(
| ||||||||||||
C、由(a+b)2=a2+2ab+b2,类比得(
| ||||||||||||
D、由|ab|=|a|•|b|,类比得|
|
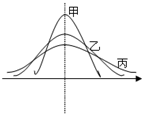 某次市教学质量检测,甲、乙、丙三科考试成绩的直方图如图所示(由于人数众多,成绩分布的直方图可视为正态分布),则由图中曲线可得下列说法中正确的一个是( )
某次市教学质量检测,甲、乙、丙三科考试成绩的直方图如图所示(由于人数众多,成绩分布的直方图可视为正态分布),则由图中曲线可得下列说法中正确的一个是( )| A、甲科总体的标准差最小 |
| B、乙科总体的标准差及平均数都居中 |
| C、丙科总体的平均数最小 |
| D、甲、乙、丙的总体的平均数不相同 |
在边长为a的正△ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=
a,这时二面角B-AD-C的大小为( )
| 1 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |