题目内容
已知数列{an}的前n项和为Sn,且满足:an+2SnSn-1=0(n≥2,n∈N*),a=
,判断{
}与{an}是否为等差数列,并说明你的理由.
| 1 |
| 2 |
| 1 |
| Sn |
考点:等差关系的确定,等差数列的性质
专题:等差数列与等比数列
分析:利用已知可得Sn≠0.利用满足:an+2SnSn-1=0(n≥2,n∈N*),可得Sn-Sn-1+2SnSn-1=0,(*).
(*)可化为
-
=2,可得{
}是以
=2为首项,2为公差的等差数列.进而得到Sn=
.
当n≥2时,an=Sn-Sn-1
-
=-
即可判断出{an}不是等差数列.
(*)可化为
| 1 |
| Sn |
| 1 |
| Sn-1 |
| 1 |
| Sn |
| 1 |
| a1 |
| 1 |
| 2n |
当n≥2时,an=Sn-Sn-1
| 1 |
| 2n |
| 1 |
| 2(n-1) |
| 1 |
| 2n(n-1) |
解答:
解:∵满足:an+2SnSn-1=0(n≥2,n∈N*),∴Sn-Sn-1+2SnSn-1=0,(*)
假设Sn=0,可得Sn-1=0,于是Sn=0对于任意正整数n都成立,而a1=
≠0,得出矛盾,故Sn≠0.
∴(*)可化为
-
=2,
∴{
}是以
=2为首项,2为公差的等差数列.
∴
=2+2(n-1)=2n,得到Sn=
.
当n≥2时,an=Sn-Sn-1
-
=-
不为等差数列.
假设Sn=0,可得Sn-1=0,于是Sn=0对于任意正整数n都成立,而a1=
| 1 |
| 2 |
∴(*)可化为
| 1 |
| Sn |
| 1 |
| Sn-1 |
∴{
| 1 |
| Sn |
| 1 |
| a1 |
∴
| 1 |
| Sn |
| 1 |
| 2n |
当n≥2时,an=Sn-Sn-1
| 1 |
| 2n |
| 1 |
| 2(n-1) |
| 1 |
| 2n(n-1) |
点评:熟练掌握an与Sn的关系、等差数列的定义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
记R为实数集,P为所有平面向量的集合,设a,b,c∈R,
,
,
∈P.则下列类比所得的结论正确的是( )
| x |
| y |
| z |
A、由a•b∈R,类比得
| ||||||||||||
B、由(ab)c=(bc)a,类比得(
| ||||||||||||
C、由(a+b)2=a2+2ab+b2,类比得(
| ||||||||||||
D、由|ab|=|a|•|b|,类比得|
|
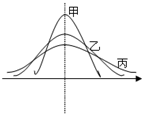 某次市教学质量检测,甲、乙、丙三科考试成绩的直方图如图所示(由于人数众多,成绩分布的直方图可视为正态分布),则由图中曲线可得下列说法中正确的一个是( )
某次市教学质量检测,甲、乙、丙三科考试成绩的直方图如图所示(由于人数众多,成绩分布的直方图可视为正态分布),则由图中曲线可得下列说法中正确的一个是( )| A、甲科总体的标准差最小 |
| B、乙科总体的标准差及平均数都居中 |
| C、丙科总体的平均数最小 |
| D、甲、乙、丙的总体的平均数不相同 |
已知函数f(x)=
,若函数g(x)=f(x)-k有两个不同的零点,则实数k的取值范围是( )
|
A、(
| ||
B、(0,
| ||
| C、(-∞,1) | ||
| D、(0,1) |
在边长为a的正△ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=
a,这时二面角B-AD-C的大小为( )
| 1 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
