题目内容
实数“a=1”是“直线l1:(a+1)x-y+1=0和l2:(2a-1)x+2y-1=0”垂直的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:先根据两直线垂直,求出a的值,即可判断
解答:
解:∵直线l1:(a+1)x-y+1=0和l2:(2a-1)x+2y-1=0垂直,
∴(a+1)(2a+1)-2=0,
解得a=-
,或a=1,
故实数“a=1”是“直线l1:(a+1)x-y+1=0和l2:(2a-1)x+2y-1=0”垂直的充分不必要条件
故选:B
∴(a+1)(2a+1)-2=0,
解得a=-
| 3 |
| 2 |
故实数“a=1”是“直线l1:(a+1)x-y+1=0和l2:(2a-1)x+2y-1=0”垂直的充分不必要条件
故选:B
点评:本题考查的知识点是充要条件,直线的一般方程与直线垂直的关系,其中当两条件直线垂直时,x,y的系数对应相乘和为0,是解答本题的关键

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
若一个等差数列首项为0,公差为2,则这个等差数列的前20项之和为( )
| A、360 | B、370 |
| C、380 | D、390 |
直线l:y=-
x+1与x轴所成夹角为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
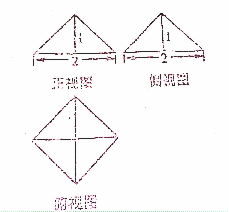 某几何体的三视图如图所示,其中正视图、侧视图均为斜边等于2的等腰直角三角形,俯视图是对角线为2的正方形,则该几何体的内切球的半径等于
某几何体的三视图如图所示,其中正视图、侧视图均为斜边等于2的等腰直角三角形,俯视图是对角线为2的正方形,则该几何体的内切球的半径等于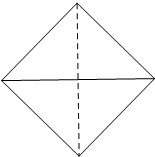 已知四面体S-ABC的所有棱长都相等,它的俯视图是一个边长为
已知四面体S-ABC的所有棱长都相等,它的俯视图是一个边长为 如图是抛物线型拱桥,在平时,水面离拱顶3米,水面宽为2
如图是抛物线型拱桥,在平时,水面离拱顶3米,水面宽为2