题目内容
以(1,1)和(2,-2)为一条直径的两个端点的圆的方程为( )
| A、x2+y2+3x-y=0 | ||
| B、x2+y2-3x+y=0 | ||
C、x2+y2-3x+y-
| ||
D、x2+y2-3x-y-
|
考点:圆的标准方程
专题:直线与圆
分析:以(1,1)和(2,-2)为直径的圆的圆心为(
,-
),半径为:r=
=
.由此能求出圆的方程.
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| (2-1)2+(-2-1)2 |
| 1 |
| 2 |
| 10 |
解答:
解:以(1,1)和(2,-2)为直径的圆的圆心为(
,-
),
半径为:r=
=
.
∴圆的方程为(x-
)2+(x+
)2=
,
整理,得x2+y2-3x+y=0.
故选:B.
| 3 |
| 2 |
| 1 |
| 2 |
半径为:r=
| 1 |
| 2 |
| (2-1)2+(-2-1)2 |
| 1 |
| 2 |
| 10 |
∴圆的方程为(x-
| 3 |
| 2 |
| 1 |
| 2 |
| 10 |
| 4 |
整理,得x2+y2-3x+y=0.
故选:B.
点评:本题考查圆的标准方程的求法,解题时要认真审题,注意圆的方程的合理运用.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
抛掷三枚质地均匀硬币,至少一次正面朝上的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,若cosA•cosB=sinA•sinB,则△ABC为( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、无法确定 |
已知f(x)是R上的奇函数,且f(1)=2,f(x+3)=f(x),则f(8)=( )
| A、2 | B、-2 | C、0 | D、2或0 |
一个正四棱锥的五个顶点都在半径为1的球面上,其中底面的四个顶点在该球的一个大圆上,则该正四棱锥的体积是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
一个算法的程序框图如图所示,若该程度输出的结果为
,则判断框①中应填入的条件是( )

| 7 |
| 12 |

| A、i<5 | B、i<4 |
| C、i>4 | D、i≤3 |
已知函数f(x)=x3+ax2+6x-9有两个极值点x1,x2,且x12+x22=5,则a=( )
A、
| ||
B、-
| ||
C、±
| ||
| D、2 |
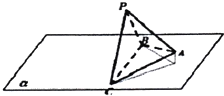 我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥.现有一正三棱锥P-ABC放置在平面α上,已知它的底面边长为2,高为h,BC在平面α上,现让它绕BC转动,并使它在某一时刻在平面α上的射影是等腰直角三角形,则h的取值范围是
我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥.现有一正三棱锥P-ABC放置在平面α上,已知它的底面边长为2,高为h,BC在平面α上,现让它绕BC转动,并使它在某一时刻在平面α上的射影是等腰直角三角形,则h的取值范围是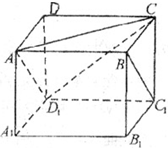 如图,正方体ABCD-A1B1C1D1,则下列四个命题:
如图,正方体ABCD-A1B1C1D1,则下列四个命题: