题目内容
证明函数f（x）=
-1在（0，+∞）上是减函数．
| 1 |
| x |
考点：函数单调性的判断与证明
专题：证明题,函数的性质及应用
分析：运用单调性的定义证明，注意取值、作差、变形和定符号、下结论几个步骤．
解答：
证明：设x1，x2是（0，+∞）上的两个任意实数，且x1＜x2，
f （x1）-f （x2）=
-1-（
-1）
=
-
=
．
因为x2-x1＞0，x1x2＞0，所以f （x1）-f （x2）＞0．即f （x1）＞f （x2），
因此 f （x）=
-1是（0，+∞）上的减函数．
f （x1）-f （x2）=
| 1 |
| x1 |
| 1 |
| x2 |
=
| 1 |
| x1 |
| 1 |
| x2 |
| x2-x1 |
| x1x2 |
因为x2-x1＞0，x1x2＞0，所以f （x1）-f （x2）＞0．即f （x1）＞f （x2），
因此 f （x）=
| 1 |
| x |
点评：本题考查函数的单调性的证明，考查定义法的运用，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知集合A={2，2a}，B={a，b}，若A∩B={1}，则A∪B为（ ）
| A、{0，1，1，2} |
| B、{1，0} |
| C、{1，2} |
| D、{0，1，2} |
若变量x，y满足约束条件
，则z=2x+y的最大值为（ ）
|
| A、5 | B、6 | C、7 | D、8 |
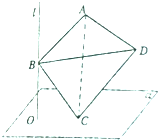如图，直线l⊥平面α，垂足为O，正四面体ABCD的棱长为8，C在平面α内，B是直线l上的动点，则当O到AD的距离为最大时，正四面体在平面α上的射影面积为（ ）A、4+2
| ||
B、16+8
| ||
C、8+8
| ||
| D、16 |
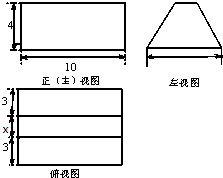现制作三视图如图所示的几何体的模型，为了配合原料，需要计算该模型的体积，而给出的俯视图中的x位置的数据丢失，但已知该模型的表面积为240，则该模型的体积为（ ）| A、200 | B、300 |
| C、400 | D、500 |