题目内容
某方程有一无理根在区间D（1，3）内，若用二分法求此根的近似值，则将D至少等分多少次后，所得近值可精确到0.1．
考点：二分法求方程的近似解
专题：计算题,函数的性质及应用
分析：每次用二分法，区间宽度减半，初始区间宽度是2，则可得第n次二等分后区间长，利用精确度，建立不等式，即可求得结论．
解答：
解：每次用二分法，区间宽度减半，初始区间宽度是2，则第n次二等分后区间长为2×
要使所得近似值的精确度达到0.1，则2×
＜0.1，解得n≥5
所以应将区间（1，3）分5次后得的近似值可精确到0.1．
| 1 |
| 2n |
要使所得近似值的精确度达到0.1，则2×
| 1 |
| 2n |
所以应将区间（1，3）分5次后得的近似值可精确到0.1．
点评：本题考查二分法求方程的根时确定精度的问题，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
要得到函数y=3sin（2x-
）的图象，只需将函数y=3sin2x的图象（ ）
| π |
| 4 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
函数f（x）=ax（a＞0且a≠1）满足f（1）＞1，则函数y=loga（x2-1）的单调减区间为（ ）
| A、（1，+∞） |
| B、（-∞，0） |
| C、（-∞，-1） |
| D、（0，+∞） |
一个空间几何体的三视图如图所示，则这个几何体的体积为 （ ）
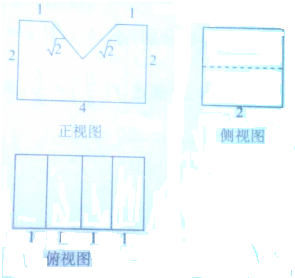
A、
| ||
| B、7 | ||
| C、14 | ||
| D、28 |