题目内容
19.已知等比数列{an},首项a1=2,公比q=3,ap+ap+1+…+ak=2178(k>p,p,k∈N+),则p+k=10.分析 通过an=2•3n-1可知ap+ap+1+…+ak=3p-1(3k-p+1-1),利用2178=32•(35-1)比较即得结论.
解答 解:依题意,an=2•3n-1,
则2178=ap+ap+1+…+ak
=$\frac{2•{3}^{p-1}(1-{3}^{k-p+1})}{1-3}$
=3p-1(3k-p+1-1),
又∵2178=9(243-1)=32•(35-1),
∴$\left\{\begin{array}{l}{p-1=2}\\{k-p+1=5}\end{array}\right.$,即$\left\{\begin{array}{l}{p=3}\\{k=7}\end{array}\right.$,
∴p+k=10,
故答案为:10.
点评 本题考查数列的求和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9. 在《九章算术》中,将有三条棱互相平行且有一个面为梯形的五面体称之为羡除,现有一个羡除如图所示,面ABC、面ABFE、面CDEF均为等腰梯形,AB∥CD∥EF,AB=6,CD=8,EF=10,EF到面ABCD的距离为3,CD与AB间的距离为10,则这个羡除的体积是( )
在《九章算术》中,将有三条棱互相平行且有一个面为梯形的五面体称之为羡除,现有一个羡除如图所示,面ABC、面ABFE、面CDEF均为等腰梯形,AB∥CD∥EF,AB=6,CD=8,EF=10,EF到面ABCD的距离为3,CD与AB间的距离为10,则这个羡除的体积是( )
 在《九章算术》中,将有三条棱互相平行且有一个面为梯形的五面体称之为羡除,现有一个羡除如图所示,面ABC、面ABFE、面CDEF均为等腰梯形,AB∥CD∥EF,AB=6,CD=8,EF=10,EF到面ABCD的距离为3,CD与AB间的距离为10,则这个羡除的体积是( )
在《九章算术》中,将有三条棱互相平行且有一个面为梯形的五面体称之为羡除,现有一个羡除如图所示,面ABC、面ABFE、面CDEF均为等腰梯形,AB∥CD∥EF,AB=6,CD=8,EF=10,EF到面ABCD的距离为3,CD与AB间的距离为10,则这个羡除的体积是( )| A. | 110 | B. | 116 | C. | 118 | D. | 120 |
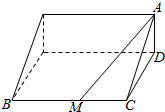 如图,某景区有一座高AD为1千米的山,山顶A处可供游客观赏日出,坡角∠ACD=30°,在山脚有一条长为10千米的小路BC,且BC与CD垂直,为方便游客,该景区拟在小路BC上找一点M,建造两条直线型公路BM和MA,其中公路BM每千米的造价为30万元,公路MA每千米造价为30万元.
如图,某景区有一座高AD为1千米的山,山顶A处可供游客观赏日出,坡角∠ACD=30°,在山脚有一条长为10千米的小路BC,且BC与CD垂直,为方便游客,该景区拟在小路BC上找一点M,建造两条直线型公路BM和MA,其中公路BM每千米的造价为30万元,公路MA每千米造价为30万元.