Question

4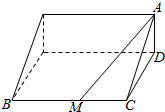．如图，某景区有一座高AD为1千米的山，山顶A处可供游客观赏日出，坡角∠ACD=30°，在山脚有一条长为10千米的小路BC，且BC与CD垂直，为方便游客，该景区拟在小路BC上找一点M，建造两条直线型公路BM和MA，其中公路BM每千米的造价为30万元，公路MA每千米造价为30万元．
（1）设∠AMC=θ，求出造价y关于θ的函数关系式；
（2）当BM长为多少米时才能使造价y最低？

Answer 1

分析 （1）通过锐角三角函数的定义易知AC=2、MC=$\frac{2}{tanθ}$、AM=$\frac{2}{sinθ}$、BM=10-$\frac{2}{tanθ}$，进而利用y=30（BM+2AM）化简即得结论；
（2）通过令y=0可知cosθ=$\frac{1}{2}$，结合α≤θ≤$\frac{π}{2}$及tanα=$\frac{1}{5}$可知θ=$\frac{π}{3}$，通过求导判定函数的单调性，进而可得结论．

解答 解：（1）在Rt△ADC中，由AD=1、∠ACD=30°可知AC=2，
在Rt△ACM中，MC=$\frac{2}{tanθ}$，AM=$\frac{2}{sinθ}$，则BM=10-$\frac{2}{tanθ}$，
设造价y的单位为千万元，则
y=30（BM+2AM）
=30（10-$\frac{2}{tanθ}$+$\frac{4}{sinθ}$）
=60（5+$\frac{2-cosθ}{sinθ}$），（α≤θ≤$\frac{π}{2}$，其中tanα=$\frac{1}{5}$）；
（2）y=60•$\frac{si{n}^{2}θ-cosθ（2-cosθ）}{si{n}^{2}θ}$=60•$\frac{1-2cosθ}{si{n}^{2}θ}$，
令y=0，得cosθ=$\frac{1}{2}$，
又∵α≤θ≤$\frac{π}{2}$，其中tanα=$\frac{1}{5}$，
∴θ=$\frac{π}{3}$，
列表：

θ	$[α，\frac{π}{3}）$	$\frac{π}{3}$	$（\frac{π}{3}，\frac{π}{2}]$
cosθ	$（\frac{1}{2}，\frac{5}{\sqrt{26}}]$	$\frac{1}{2}$	$[0，\frac{1}{2}）$
y′	-	0	+
y	↓	最小值	↑

∴当θ=$\frac{π}{3}$时y有最小值，此时BM=10-$\frac{2\sqrt{3}}{3}$．
答：当BM长为（10-$\frac{2\sqrt{3}}{3}$）米时才能使造价y最低．

点评 本题考查函数模型的选择与应用，考查分析问题、解决问题的能力，注意解题方法的积累，属于中档题．