题目内容
3．函数$y={（{\frac{1}{2}}）^x}-2$的图象一定经过（ ）| A． | 第一、二、三象限 | B． | 第一、二、四象限 | C． | 第一、三、四象限 | D． | 第二、三、四象限 |
分析 根据函数$y={（{\frac{1}{2}}）^x}-2$为减函数，且图象经过（-2，2）、（0，-1），可得它的图象经过第二、三、四象限．
解答 解：函数$y={（{\frac{1}{2}}）^x}-2$为减函数，且图象经过（-2，2）、（0，-1），
故它的图象经过第二、三、四象限，
故选：D．
点评 本题主要考查函数的单调性，函数的图象特征，属于基础题．
练习册系列答案
相关题目
11．函数$y={x^2}+\frac{1}{x}+1$在x=1处的切线方程是（ ）
| A． | x-y+2=0 | B． | x-y-4=0 | C． | x+y-4=0 | D． | x+y+2=0 |
8．若角α=2rad（rad为弧度制单位），则下列说法错误的是（ ）
| A． | 角α为第二象限角 | B． | α=$\frac{360°}{π}$ | C． | sinα＞0 | D． | sinα＜cosα |
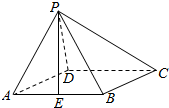如图，在四棱锥P-ABCD中，底面ABCD是菱形，PA=PB，且侧面PAB⊥平面ABCD，点E是AB的中点．