题目内容
记Cir为从i个不同的元素中取出r个元素的所有组合的个数.随机变量ξ表示满足Cir≤
i2的二元数组(r,i)中的r,其中i∈{2,3,4,5,6,7,8,9,10},每一个Cir(r=0,1,2,…,i)都等可能出现.求Eξ.
| 1 |
| 2 |
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:由已知得当r=0,1,2,i-2,i-1,i时,
≤
i2成立,当r=3,…,i-3时,
>
i2,由此能求出Eξ.
| C | r i |
| 1 |
| 2 |
| C | r i |
| 1 |
| 2 |
解答:
解:∵
≤
i2,
当i≥2时,
=
=1≤
i2,
=
=i≤
i2,
=
=
≤
i2,
≤
,
∴当2≤i≤5,i∈N*时,
≤
i2的解为r=0,1,…,i.…(3分)
当6≤i≤10,i∈N*,
≥
?r≤
,
由
=
≤
i2?i=3,4,5可知:
当r=0,1,2,i-2,i-1,i时,
≤
i2成立,
当r=3,…,i-3时,
≥
≥
i2(等号不同时成立),即
>
i2.…(6分)
∴ξ的分布列为:
…(8分)
∴Eξ=(0+1+2)×
+(3+4+5+6+7+8)×
+9×
+10×
=
.…(10分)
| C | r i |
| 1 |
| 2 |
当i≥2时,
| C | 0 i |
| C | i i |
| 1 |
| 2 |
| C | 1 i |
| C | i-1 i |
| 1 |
| 2 |
| C | 2 i |
| C | i-2 i |
| i(i-1) |
| 2 |
| 1 |
| 2 |
| C | 3 5 |
| 52 |
| 2 |
∴当2≤i≤5,i∈N*时,
| C | r i |
| 1 |
| 2 |
当6≤i≤10,i∈N*,
| C | r+1 i |
| C | r i |
| i-1 |
| 2 |
由
| C | 3 i |
| i(i-1)(i-2) |
| 6 |
| 1 |
| 2 |
当r=0,1,2,i-2,i-1,i时,
| C | r i |
| 1 |
| 2 |
当r=3,…,i-3时,
| C | r i |
| C | 3 i |
| 1 |
| 2 |
| C | r i |
| 1 |
| 2 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||||||||||||||||||||
| P(ξ) |
|
|
|
|
|
|
|
|
|
|
|
∴Eξ=(0+1+2)×
| 3 |
| 16 |
| 1 |
| 16 |
| 1 |
| 24 |
| 1 |
| 48 |
| 77 |
| 24 |
点评:本题考查离散型随机变量的数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
某商店一个月的收支数据为a1,a2,…aN,按程序框图进行统计,那么关于S,T的关系正确的是( )
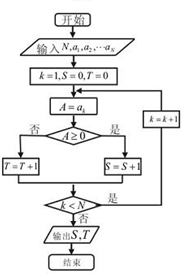

| A、N=S-T | B、N=S+T |
| C、S≥T | D、S≤T |
下列推断错误的是( )
| A、命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1则x2-3x+2≠0” |
| B、命题p:存在x0∈R,使得x02+x0+1<0,则非p:任意x∈R,都有x2+x+1≥0 |
| C、若p且q为假命题,则p,q均为假命题 |
| D、“x<1”是“x2-3x+2>0”的充分不必要条件 |