题目内容
函数f（x）在R上可导，且f′（0）=2．?x，y∈R，若函数f（x+y）=f（x）f（y）成立，则f（0）= ．
考点：抽象函数及其应用,导数的运算
专题：函数的性质及应用
分析：由于y与x无关，不是x的函数，故两边对x求导，可得f'（x+y）=f'（x）+4y，对x，y赋值后，即可得到f'（t）=4t-2，令其为0，解出即可．
解答：
解：由于R上的可导函数f（x）满足f（x+y）=f（x）f（y）（x，y∈R），
故两边对x求导，f'（x+y）=f'（x）f（y）．
x=0，y=0带入，f'（0）=f'（0）f（0）．
f′（0）=2．
解得f（0）=1．
故答案为：1；
故两边对x求导，f'（x+y）=f'（x）f（y）．
x=0，y=0带入，f'（0）=f'（0）f（0）．
f′（0）=2．
解得f（0）=1．
故答案为：1；
点评：本题考查抽象函数及导数的运算，属于基本知识的考查．
练习册系列答案
相关题目
，70），[70，80），[80，90），[90，100]．
最新调查显示，目前我国主流城市白领亚健康的比例高达76%，处于过度疲劳状态的接近6成，大部分白领均缺乏运动锻炼．某健康协会为了了解白领们每天锻炼身体的时间（单位：分钟），进入一些国企中随机抽取了n名白领进行调查，其频率分布直方图如图所示，其中运动时间不低于20分钟的人数为81人，则n的值为
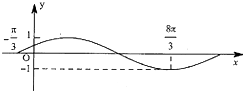将函数y=sinx图象上点的横坐标扩大到原来的m倍，纵坐标保持不变，再向左平移n个单位得到如图所示函数的图象，则m，n可以为（ ）A、m=2，n=
| ||
B、m=2，n=
| ||
C、m=4，n=
| ||
D、m=4，n=
|
在等分区间的情况下，f（x）=
（x∈[0，2]）及x轴所围成的曲边梯形的面积和式的极限形式正确的是（ ）
| 1 |
| 1+x2 |
A、
| |||||||||||
B、
| |||||||||||
C、
| |||||||||||
D、
|
已知a＞1，e=2.71828…是自然对数的底数，若函数y=logax与y=ax的图象与直线y=x相切于同一点，则a=（ ）
| A、ee | ||
| B、e2 | ||
| C、e | ||
D、e
|