题目内容
已知F2、F1是双曲线
-
=1(a>0,b>0)的上、下焦点,点F2关于渐近线的对称点恰好落在以F1为圆心,|OF1|为半径的圆上,则双曲线的离心率为( )
| y2 |
| a2 |
| x2 |
| b2 |
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:首先求出F2到渐近线的距离,利用F2关于渐近线的对称点恰落在以F1为圆心,|OF1|为半径的圆上,可得直角三角形MF1F2,运用勾股定理,即可求出双曲线的离心率.
解答:
解:由题意,F1(0,-c),F2(0,c),
一条渐近线方程为y=
x,则F2到渐近线的距离为
=b.
设F2关于渐近线的对称点为M,F2M与渐近线交于A,
∴|MF2|=2b,A为F2M的中点,
又0是F1F2的中点,∴OA∥F1M,∴∠F1MF2为直角,
∴△MF1F2为直角三角形,
∴由勾股定理得4c2=c2+4b2
∴3c2=4(c2-a2),∴c2=4a2,
∴c=2a,∴e=2.
故选C.
一条渐近线方程为y=
| a |
| b |
| bc | ||
|
设F2关于渐近线的对称点为M,F2M与渐近线交于A,
∴|MF2|=2b,A为F2M的中点,
又0是F1F2的中点,∴OA∥F1M,∴∠F1MF2为直角,
∴△MF1F2为直角三角形,
∴由勾股定理得4c2=c2+4b2
∴3c2=4(c2-a2),∴c2=4a2,
∴c=2a,∴e=2.
故选C.
点评:本题主要考查了双曲线的几何性质以及有关离心率和渐近线,考查勾股定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
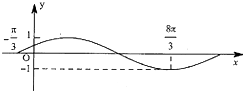 将函数y=sinx图象上点的横坐标扩大到原来的m倍,纵坐标保持不变,再向左平移n个单位得到如图所示函数的图象,则m,n可以为( )
将函数y=sinx图象上点的横坐标扩大到原来的m倍,纵坐标保持不变,再向左平移n个单位得到如图所示函数的图象,则m,n可以为( )A、m=2,n=
| ||
B、m=2,n=
| ||
C、m=4,n=
| ||
D、m=4,n=
|
在等分区间的情况下,f(x)=
(x∈[0,2])及x轴所围成的曲边梯形的面积和式的极限形式正确的是( )
| 1 |
| 1+x2 |
A、
| |||||||||||
B、
| |||||||||||
C、
| |||||||||||
D、
|
 最新调查显示,目前我国主流城市白领亚健康的比例高达76%,处于过度疲劳状态的接近6成,大部分白领均缺乏运动锻炼.某健康协会为了了解白领们每天锻炼身体的时间(单位:分钟),进入一些国企中随机抽取了n名白领进行调查,其频率分布直方图如图所示,其中运动时间不低于20分钟的人数为81人,则n的值为
最新调查显示,目前我国主流城市白领亚健康的比例高达76%,处于过度疲劳状态的接近6成,大部分白领均缺乏运动锻炼.某健康协会为了了解白领们每天锻炼身体的时间(单位:分钟),进入一些国企中随机抽取了n名白领进行调查,其频率分布直方图如图所示,其中运动时间不低于20分钟的人数为81人,则n的值为



