题目内容
1.如图,四边形ABCD是圆柱的轴截面,E是底面圆周上异于A、B的一点,则下面结论中错误的是( )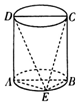
| A. | AE⊥CE | B. | BE⊥DE | C. | DE⊥CE | D. | 面ADE⊥面BCE |
分析 由AB是底面圆的直径,可得AE⊥EB.由四边形ABCD是圆柱的轴截面,可得AD⊥底面AEB,BC⊥底面AEB.再利用线面面面垂直的判定与性质定理即可得出.
解答 解:由AB是底面圆的直径,则∠AEB=$\frac{π}{2}$,即AE⊥EB.
∵四边形ABCD是圆柱的轴截面,∴AD⊥底面AEB,BC⊥底面AEB.
可得:BE⊥DE,因此BE⊥平面ADE.
同理可得:AE⊥CE,平面BCE⊥平面ADE.
可得A,B,D正确.
而DE⊥CE不正确.
故选:C.
点评 本题考查了线面面面垂直的判定与性质定理、圆柱的轴截面的性质、圆的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.若3m=b,则${log_{3^2}}b$=( )
| A. | 2m | B. | $\frac{m}{2}$ | C. | m2 | D. | $\sqrt{m}$ |
6.在△ABC中,已知a=17,b=24,A=45°,则此三角形( )
| A. | 无解 | B. | 有两解 | C. | 有一解 | D. | 解的个数不确定 |

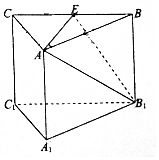 如图,在直棱柱ABC-A1B1C1中,AB=AC=4,∠BAC=90°,E为BC的中点.
如图,在直棱柱ABC-A1B1C1中,AB=AC=4,∠BAC=90°,E为BC的中点.