题目内容
已知Rt△ABC的两条直角边的边长分别为3和4,若以其中一条直角边为轴旋转一周,则所形成的几何体的体积为( )
| A、16π |
| B、12π或16π |
| C、36π |
| D、36π或48π |
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:根据圆锥的展开图可知,直角三角形沿直角边旋转一周得到的是一个圆锥,根据题干可得:圆锥的底面半径为3高为4;或者底面半径为4高为3,由此利用圆锥的体积公式计算出它们的体积即可解答.
解答:
解:底面半径为3高为4的圆锥的体积为:
×π×32×4,
=12π,
底面半径为4高为3的圆锥的体积为:
×π×42×3,
=16π,
故选:B.
| 1 |
| 3 |
=12π,
底面半径为4高为3的圆锥的体积为:
| 1 |
| 3 |
=16π,
故选:B.
点评:根据圆锥的特点,得出旋转一周后得到的是一个圆锥是解决此类问题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
若直线l1:y=kx+1与l2:x-y-1=0的交点在第一象限内,则k的取值范围是( )
| A、k>1 |
| B、-1<k<1 |
| C、k<-1或k>1 |
| D、k<-1 |
对于函数y=sin(2x),下面说法中正确的是( )
| A、函数是周期为π的奇函数 |
| B、函数是周期为π的偶函数 |
| C、函数是周期为2π的奇函数 |
| D、函数是周期为2π的偶函数 |
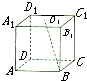 如图,正方体A1B1C1D1-ABCD中,O1是上底面A1B1C1D1的中心,若正方体的棱长为2,则O1B与CD所成角的余弦值为( )
如图,正方体A1B1C1D1-ABCD中,O1是上底面A1B1C1D1的中心,若正方体的棱长为2,则O1B与CD所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知{an},{bn}都是等比数列,它们的前n项和分别为Sn,Tn,且
=
对n∈N*恒成立,则
=( )
| Sn |
| Tn |
| 3n+1 |
| 4 |
| an+1 |
| bn+1 |
| A、3n | ||
| B、4n | ||
| C、3n或4n | ||
D、(
|
如图,D是直角△ABC斜边BC上一点,若AB=AD,AC=
DC,则sin∠ABD=( )
| 3 |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在等差数列{an}中,a14=
,a114=
,a2014=
,则ab+19bc-20ac=( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| A、0 | B、14 |
| C、114 | D、2014 |
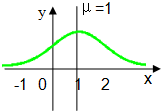 在对我市高中学生某项身体素质的测试中,测试结果ξ服从正态分布N(1,σ2)(σ>0)(如图),若ξ在(0,2)内取值的概率为0.8,则ξ在(0,1)内取值的概率为
在对我市高中学生某项身体素质的测试中,测试结果ξ服从正态分布N(1,σ2)(σ>0)(如图),若ξ在(0,2)内取值的概率为0.8,则ξ在(0,1)内取值的概率为