题目内容
若C
=C
+C
，则n= ．
3 n |
3 n-1 |
4 n-1 |
考点：组合及组合数公式
专题：概率与统计
分析：利用组合数公式求解．
解答：
解：∵C
=C
+C
，
∴
=
+
，
整理，得n2-7n=0，
解得n=7或n=0（舍）．
故答案为：7．
3 n |
3 n-1 |
4 n-1 |
∴
| n(n-1)(n-2) |
| 3×2×1 |
| (n-1)(n-2)(n-3) |
| 3×2×1 |
| (n-1)(n-2)(n-3)(n-4) |
| 4×3×2×1 |
整理，得n2-7n=0，
解得n=7或n=0（舍）．
故答案为：7．
点评：本题考查组合数公式的应用，解题时要认真审题，是基础题．
练习册系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
设n是自然数，f（n）=1+
+
+…+
，经计算可得，f（2）=
，f（4）＞2，f（8）＞
，f（16）＞3，f（32）＞
．观察上述结果，可得出的一般结论是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
A、f（2n）＞
| ||
B、f（n2）≥
| ||
C、f（2n）≥
| ||
D、f(2n)＞
|
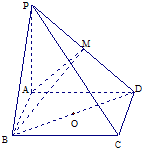如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2．BM⊥PD于M．