Question

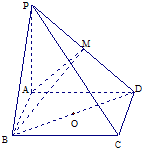如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2．BM⊥PD于M．
（1）求证：平面ABM⊥平面PCD；
（2）求直线PC与平面ABM所成的角的正切值；
（3）求点O到平面ABM的距离．

Answer 1

考点：平面与平面垂直的判定,直线与平面所成的角,点、线、面间的距离计算

专题：空间位置关系与距离,空间角

分析：（1）由直径性质得BM⊥PD．由线面垂直得PA⊥AB，又AB⊥AD，由此能证明PD⊥平面ABM，从而得到平面ABM⊥平面PCD．
（2）设平面ABM与PC交于点N，因为AB∥CD，所以AB∥平面PCD，从而AB∥MN∥CD，所以∠PNM就是PC与平面ABM所成的角，由此能求出直线PC与平面ABM所成的角的正切值．
（3）由O是BD的中点，得O点到平面ABM的距离等于D点到平面ABM距离的一半，由PD⊥平面ABM于M，知|DM|就是D点到平面ABM距离．

解答： （1）证明：依题设，M在以BD为直径的球面上，则BM⊥PD．
因为PA⊥平面ABCD，则PA⊥AB，又AB⊥AD，
所以AB⊥平面PAD，则AB⊥PD，
因此有PD⊥平面ABM，
所以平面ABM⊥平面PCD．
（2）解：设平面ABM与PC交于点N，因为AB∥CD，所以AB∥平面PCD，
则AB∥MN∥CD，
由（1）知，PD⊥平面ABM，则MN是PN在平面ABM上的射影，
所以∠PNM就是PC与平面ABM所成的角，且∠PNM=∠PCD．
tan∠PNM=tan∠PCD=

PD

DC

=2

2

．
（3）解：因为O是BD的中点，
则O点到平面ABM的距离等于D点到平面ABM距离的一半，
由（1）知，PD⊥平面ABM于M，
则|DM|就是D点到平面ABM距离．
因为在Rt△PAD中，PA=AD=4，PD⊥AM，
所以M为PD中点，DM=2

2

，
则O点到平面ABM的距离等于

2

．

点评：本题考查平面与平面垂直的证明，考查直线与平面所成角的正切值的求法，考查点到平面的距离的求法，解题时要认真审题，注意空间思维能力的培养．