题目内容
已知f(x)=
-(a+1)x2+4x+1(a∈R)
(1)当a=-1时,求函数的单调区间;
(2)当a∈R时,讨论函数的单调增区间;
(3)是否存在负实数a,使x∈[-1,0],函数有最小值-3?
| ax3 |
| 3 |
(1)当a=-1时,求函数的单调区间;
(2)当a∈R时,讨论函数的单调增区间;
(3)是否存在负实数a,使x∈[-1,0],函数有最小值-3?
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,分类讨论,导数的综合应用
分析:(1)写出a=-1的函数解析式,再求导,分别令大于0,小于0,得到单调区间;
(2)求出导数,分解因式,对a讨论,分a=0,a<0,0<a<1,a=1,a>1五种情况,求出单调增区间;
(3)假设存在负实数a,使x∈[-1,0],函数有最小值-3.再由a≥-2,a≤-2,讨论单调区间,得到最小值,再解出a,检验,即可得到答案.
(2)求出导数,分解因式,对a讨论,分a=0,a<0,0<a<1,a=1,a>1五种情况,求出单调增区间;
(3)假设存在负实数a,使x∈[-1,0],函数有最小值-3.再由a≥-2,a≤-2,讨论单调区间,得到最小值,再解出a,检验,即可得到答案.
解答:
解:(1)当a=-1时,f(x)=-
x3+4x+1,f′(x)=-x2+4,
由f′(x)<0,解得x>2或x<-2;
由f′(x)>0,解得-2<x<2,
故函数的单调减区间为:(-∞,-2),(2,+∞),单调增区间为:(-2,2);
(2)f′(x)=ax2-2(a+1)x+4=(ax-2)(x-2),
①当a=0,由f′(x)>0得到x<-2,即增区间为(-∞,-2);
②当a<0,f′(x)>0,得到
<x<2,即增区间为(
,2);
③当0<a<1,f′(x)>0,得到x>
或x<2,即增区间为(-∞,2),(
,+∞),
④当a=1,f(x)=(x-2)2≥0,即增区间为(-∞,+∞);
⑤当a>1,f′(x)>0,得到x<
或x>2,即增区间为(2,+∞),(-∞,
).
(3)假设存在负实数a,使x∈[-1,0],函数有最小值-3.
因a<0,由②分两类(依据:单调性,极小值点是否在区间[-1,0]上是分类“契机”):
①当
≤-1?a≥-2,当x∈[-1,0)⊆(
,2),f(x)递增,f(x)min=f(-1)=-3,
即-
-(a+1)-3=-3,解得a=-
>-2;
②当
≥-1?a≤-2,由单调性知:f(x)min=f(
)=-3,化简得:3a2+3a-1=0,解得
a=
>-2,不合要求.
综上,存在这样的负数a,且a=-
为所求.
| 1 |
| 3 |
由f′(x)<0,解得x>2或x<-2;
由f′(x)>0,解得-2<x<2,
故函数的单调减区间为:(-∞,-2),(2,+∞),单调增区间为:(-2,2);
(2)f′(x)=ax2-2(a+1)x+4=(ax-2)(x-2),
①当a=0,由f′(x)>0得到x<-2,即增区间为(-∞,-2);
②当a<0,f′(x)>0,得到
| 2 |
| a |
| 2 |
| a |
③当0<a<1,f′(x)>0,得到x>
| 2 |
| a |
| 2 |
| a |
④当a=1,f(x)=(x-2)2≥0,即增区间为(-∞,+∞);
⑤当a>1,f′(x)>0,得到x<
| 2 |
| a |
| 2 |
| a |
(3)假设存在负实数a,使x∈[-1,0],函数有最小值-3.
因a<0,由②分两类(依据:单调性,极小值点是否在区间[-1,0]上是分类“契机”):
①当
| 2 |
| a |
| 2 |
| a |
即-
| a |
| 3 |
| 3 |
| 4 |
②当
| 2 |
| a |
| 2 |
| a |
a=
-3±
| ||
| 6 |
综上,存在这样的负数a,且a=-
| 3 |
| 4 |
点评:本题考查导数的综合运用:求单调区间和函数的最值,同时考查分类讨论思想方法,考查存在型问题的解法,是一道综合题.

练习册系列答案
相关题目
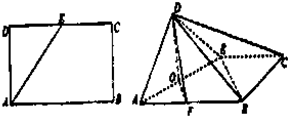 已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△ADE折起,使平面ADE上平面ABCE,点O、F分别是AE、AB的中点.
已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△ADE折起,使平面ADE上平面ABCE,点O、F分别是AE、AB的中点.