题目内容
以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C1的极坐标方程为ρ2+6ρcosθ-2ρsinθ+6=0,曲线C2的参数方程为
(θ为参数).
(Ⅰ)将曲线C1的极坐标方程化为直角坐标方程;
(Ⅱ)若曲线C1与曲线C2交于A,B两点,求|AB|的长.
|
(Ⅰ)将曲线C1的极坐标方程化为直角坐标方程;
(Ⅱ)若曲线C1与曲线C2交于A,B两点,求|AB|的长.
考点:参数方程化成普通方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(Ⅰ)根据ρ2=x2+y2,x=ρcosθ,y=ρsinθ和条件,将曲线C1的极坐标方程化为直角坐标方程;
(Ⅱ)利用平方关系消去θ得到曲线C2的直角坐标方程,将两个圆的方程相减得的直线AB的方程,利用弦长公式和点到直线的距离公式求出|AB|的长.
(Ⅱ)利用平方关系消去θ得到曲线C2的直角坐标方程,将两个圆的方程相减得的直线AB的方程,利用弦长公式和点到直线的距离公式求出|AB|的长.
解答:
解:(Ⅰ)∵曲线C1的极坐标方程为ρ2+6ρcosθ-2ρsinθ+6=0,
且ρ2=x2+y2,x=ρcosθ,y=ρsinθ,
∴曲线C1的直角坐标方程为x2+y2+6x-2y+6=0;…(3分)
(Ⅱ)由
知,
两个方程平方相加得,曲线C2的直角坐标方程为x2+y2=9,
圆C1的方程减去圆C2的方程得:6x-2y+15=0,
∴公共弦所在的直线AB的方程为6x-2y+15=0,
∴公共弦|AB|=2
=
.…(7分)
且ρ2=x2+y2,x=ρcosθ,y=ρsinθ,
∴曲线C1的直角坐标方程为x2+y2+6x-2y+6=0;…(3分)
(Ⅱ)由
|
两个方程平方相加得,曲线C2的直角坐标方程为x2+y2=9,
圆C1的方程减去圆C2的方程得:6x-2y+15=0,
∴公共弦所在的直线AB的方程为6x-2y+15=0,
∴公共弦|AB|=2
9-(
|
3
| ||
| 2 |
点评:本小题考查了参数方程、极坐标方程,公共弦所在的直线方程的求法,以及弦长公式和点到直线的距离公式等基础知识,考查运算求解能力.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
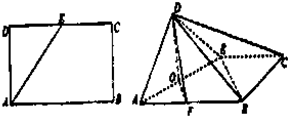 已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△ADE折起,使平面ADE上平面ABCE,点O、F分别是AE、AB的中点.
已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△ADE折起,使平面ADE上平面ABCE,点O、F分别是AE、AB的中点.