题目内容
1.已知函数$f(x)=1-x+{log_2}\frac{1-x}{1+x}$,则$f({\frac{1}{2}})+f({-\frac{1}{2}})$的值为( )| A. | 0 | B. | -2 | C. | 2 | D. | $2{log_2}\frac{1}{3}$ |
分析 由题意分别求出f($\frac{1}{2}$)和f(-$\frac{1}{2}$),由此能求出$f({\frac{1}{2}})+f({-\frac{1}{2}})$的值.
解答 解:∵函数$f(x)=1-x+{log_2}\frac{1-x}{1+x}$,
∴f($\frac{1}{2}$)=1-$\frac{1}{2}+lo{g}_{2}\frac{1-\frac{1}{2}}{1+\frac{1}{2}}$=$\frac{1}{2}+lo{g}_{2}\frac{1}{3}$,
f(-$\frac{1}{2}$)=1+$\frac{1}{2}+lo{g}_{2}\frac{1+\frac{1}{2}}{1-\frac{1}{2}}$=$\frac{3}{2}+lo{g}_{2}3$,
∴$f({\frac{1}{2}})+f({-\frac{1}{2}})$=$\frac{1}{2}+lo{g}_{2}\frac{1}{3}+\frac{3}{2}+lo{g}_{2}3$=2.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
12.已知圆P的半径等于椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1的长轴长,圆心是抛物线y2=4$\sqrt{2}$x的焦点,经过点M(-$\sqrt{2}$,1)的直线1将圆P分成两段弧,则劣弧长度的最小值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | 2π | D. | 4π |
9.已知偶函数f(x)在区间[0,+∞)单调递减,则满足 $f(2x-1)>f(\frac{1}{3})$的实数x的取值范围是( )
| A. | ($\frac{1}{3}$,$\frac{2}{3}$) | B. | [$\frac{1}{3}$,$\frac{2}{3}$) | C. | ($\frac{1}{2}$,$\frac{2}{3}$) | D. | [$\frac{1}{2}$,$\frac{2}{3}$) |
11.如图所示的程序框图,输出的值为( )
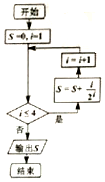

| A. | $\frac{15}{16}$ | B. | $\frac{15}{12}$ | C. | $\frac{13}{8}$ | D. | $\frac{13}{4}$ |