题目内容
若函数f(x)=log
(x2-ax+1)
(1)若函数的定义域为R,求a的取值范围;
(2)若函数的值域为R,求a的取值范围;
(3)若函数在(-∞,1-
)上是增函数,求a的取值范围.
| 1 |
| 2 |
(1)若函数的定义域为R,求a的取值范围;
(2)若函数的值域为R,求a的取值范围;
(3)若函数在(-∞,1-
| 3 |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:(1)由对数的真数大于零和题意得:x2-ax+1>0对任意x∈R都成立,则△<0,再求出实数a的取值范围;
(2)函数f(x)的值域为R,说明对数的真数取到所有的正数,可得△≥0,求出实数a的取值范围;
(3)设t=x2-ax+1,由复合函数单调性、对数的真数大于零列出不等式组,求出a的取值范围.
(2)函数f(x)的值域为R,说明对数的真数取到所有的正数,可得△≥0,求出实数a的取值范围;
(3)设t=x2-ax+1,由复合函数单调性、对数的真数大于零列出不等式组,求出a的取值范围.
解答:
解:(1)由题意得,x2-ax+1>0对任意x∈R都成立,
则△=a2-4<0,解得-2<a<2
所以a的取值范围是(-2,2);
(2)要使函数的值域是R,只要△=a2-4≥0,得a≤-2或a≥2,
所以a的取值范围(-∞,-2]∪[2,+∞);
(3)设t=x2-ax+1,则函数y=log
t(t>0)在定义域上是减函数,
因为函数f(x)在(-∞,1-
)上是增函数,
所以函数t=x2-ax+1在(-∞,1-
)上是减函数,
则
,
解得a≥2(1-
),
所以a的取值范围是[2(1-
),+∞).
则△=a2-4<0,解得-2<a<2
所以a的取值范围是(-2,2);
(2)要使函数的值域是R,只要△=a2-4≥0,得a≤-2或a≥2,
所以a的取值范围(-∞,-2]∪[2,+∞);
(3)设t=x2-ax+1,则函数y=log
| 1 |
| 2 |
因为函数f(x)在(-∞,1-
| 3 |
所以函数t=x2-ax+1在(-∞,1-
| 3 |
则
|
解得a≥2(1-
| 3 |
所以a的取值范围是[2(1-
| 3 |
点评:本题考查对数函数的性质,复合函数单调性,掌握对数函数的性质及一元二次函数的性质是解决本题的关键.

练习册系列答案
相关题目
关于函数f(x)=ax(0<a<1),下列说法正确的是( )
| A、定义域为R+ |
| B、值域为R+ |
| C、图象关于x轴对称 |
| D、为增函数 |
如果f(x)的定义域为R,f(x+2)=f(x+1)-f(x),且f(1)=lg3-lg2,f(2)=lg3+lg5,则f(2008)=( )
| A、1 | B、-1 |
| C、lg2-lg3 | D、-lg3-lg5 |
 如图所示,已知空间四边形ABCD,连结AC,BD,E,F,G分别是BC,CD,DB的中点,请化简:
如图所示,已知空间四边形ABCD,连结AC,BD,E,F,G分别是BC,CD,DB的中点,请化简:
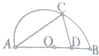 如图,某风景区准备美化以快直径为AB的半圆形空地,O为圆心,C为圆周上一点,CD⊥AB于D,已知AB为一假山壁,若以山壁为一边,△ACD内为一喷泉,△ACD外栽种花草,若AB=200米,∠CAB=θ,y=AC+CD.
如图,某风景区准备美化以快直径为AB的半圆形空地,O为圆心,C为圆周上一点,CD⊥AB于D,已知AB为一假山壁,若以山壁为一边,△ACD内为一喷泉,△ACD外栽种花草,若AB=200米,∠CAB=θ,y=AC+CD.