题目内容
已知数列{an}中，a1=2，a8=58，an+1=an+cn（c为常数），则c的值是 ．
考点：等差数列的性质
专题：等差数列与等比数列
分析：在已知递推式中分别取n=1，2，…，7，得到7个等式，然后利用累加法得到a8=a1+28c，再代入已知条件求得c．
解答：
解：在数列{an}中，
∵an+1=an+cn，
∴a2=a1+c，
a3=a2+2c，
…
a8=a7+7c，
累加得：a8=a1+（c+2c+…+7c）=a1+
=a1+28c，
又a1=2，a8=58，
∴58=2+28c，即c=2．
故答案为：2．
∵an+1=an+cn，
∴a2=a1+c，
a3=a2+2c，
…
a8=a7+7c，
累加得：a8=a1+（c+2c+…+7c）=a1+
| (c+7c)×7 |
| 2 |
又a1=2，a8=58，
∴58=2+28c，即c=2．
故答案为：2．
点评：本题考查了数列递推式，考查了累加法求数列的通项公式，是基础题．
练习册系列答案
相关题目
已知函数f（x）=x+ln （
+x），g（x）=
，则（ ）
| x2+1 |
|
| A、f（x）是奇函数，g（x）是奇函数 |
| B、f（x）是偶函数，g（x）是偶函数 |
| C、f（x）是奇函数，g（x）是偶函数 |
| D、f（x）是偶函数，g（x）是奇函数 |
圆x2+y2-4y=0的圆心坐标和半径分别为（ ）
| A、（0，2），2 |
| B、（0，-2），2 |
| C、（-2，0），2 |
| D、（2，0），2 |
已知sinα-cosα=
，α∈（0，π），则tanα=（ ）
| 2 |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、
|
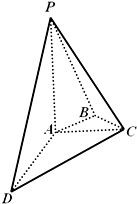如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1．