题目内容
3.设命题q:对任意实数x,不等式x2-2x+m≥0恒成立;命题q:方程$\frac{x^2}{m-3}-\frac{y^2}{m}=1$表示焦点在x轴上的双曲线.(1)若命题q为真命题,求实数m的取值范围;
( 2)若命题:“p∨q”为真命题,且“p∧q”为假命题,求实数m的取值范围.
分析 (1)由方程$\frac{x^2}{m-3}-\frac{y^2}{m}=1$表示焦点在x轴上的双曲线.可得$\left\{\begin{array}{l}m-3>0\\ m>0\end{array}\right.$,得m范围.
(2)由不等式x2-2x+m≥0恒成立,可得△≤0,由p∧q为假命题,p∨q为真命题,可得p,q一真一假.
解答 解:(1)∵方程$\frac{x^2}{m-3}-\frac{y^2}{m}=1$表示焦点在x轴上的双曲线.
∴$\left\{\begin{array}{l}m-3>0\\ m>0\end{array}\right.$,得m>3;
∴当m>3时,q为真命题.
(2)∵不等式x2-2x+m≥0恒成立∴△=4-4m≤0,
∴m≥1,∴当m≥1时,p为真命题.
∵p∧q为假命题,p∨q为真命题,∴p,q一真一假;
①当p真q假$\left\{\begin{array}{l}m≥1\\ m≤3\end{array}\right.⇒1≤m≤3$.
②当p假q真$\left\{\begin{array}{l}m<1\\ m>3\end{array}\right.$,无解.
综上,m的取值范围是[1,3].
点评 本题考查了不等式的解法、双曲线的标准方程及其性质、复合命题真假的判定及其应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.三棱锥P-ABC中,PA⊥底面ABC,PA=3,底面ABC是边长为2的正三角形,则三棱锥P-ABC的体积等于( )
| A. | 3$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
15.圆x2+y2=4与圆x2+y2-4y+3=0的位置关系是( )
| A. | 相离 | B. | 相交 | C. | 外切 | D. | 内切 |
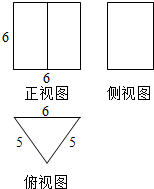 某几何体的三视图如图所示,其中正视图是边长为6的正方形,俯视图是腰长为5,底边长为6的等腰三角形,则该几何体的体积是72,表面积是120.
某几何体的三视图如图所示,其中正视图是边长为6的正方形,俯视图是腰长为5,底边长为6的等腰三角形,则该几何体的体积是72,表面积是120.