题目内容
12.F(1,0)为一定点,P(0,b)是y轴上的一动点,x轴上的点M满足$\overrightarrow{PM}$•$\overrightarrow{PF}$=0,若点N满足2$\overrightarrow{PN}$+$\overrightarrow{NM}$=0,求:(1)点N的轨迹曲线C的方程;
(2)曲线C的任何两条相互垂直的切线的交点轨迹.
分析 (1)由2$\overrightarrow{PN}$+$\overrightarrow{NM}$=0可知M,N关于点P对称,设N(x,y)得出M点坐标,求得$\overrightarrow{PM}$,$\overrightarrow{PN}$的坐标,代入数量积公式整理得出轨迹方程;
(2)设交点坐标为(x0,y0),切线斜率为k,联立方程组消元,令判别式△=0得出关于k的方程,根据切线垂直和根与系数的关系得到x0,y0的关系,即轨迹方程.
解答 解:(1)∵2$\overrightarrow{PN}$+$\overrightarrow{NM}$=0,∴点M,N关于点P对称,
设N(x,y),则M(-x,2b-y),∵M在x轴上,∴y=2b,即b=$\frac{y}{2}$.
$\overrightarrow{PM}$=(-x,-b),$\overrightarrow{PF}$=(1,-b),∵$\overrightarrow{PM}$•$\overrightarrow{PF}$=0,∴-x+b2=0,∴-x+$\frac{{y}^{2}}{4}$=0,即y2=4x.
∴点N的轨迹曲线C的方程是y2=4x.
(2)设曲线C的两条互相垂直的垂线的交点坐标为(x0,y0),切线的斜率为k,则切线方程为y-y0=k(x-x0),
联立方程组$\left\{\begin{array}{l}{y-{y}_{0}=k(x-{x}_{0})}\\{{y}^{2}=4x}\end{array}\right.$,消元得:$\frac{k}{4}$y2-y+y0-kx0=0,
∴△=1-k(y0-kx0)=0,即x0k2-y0k+1=0.∴k1k2=$\frac{1}{{x}_{0}}$=-1,∴x0=-1.
曲线C的任何两条相互垂直的切线的交点轨迹是直线x=-1.
点评 本题考查了直线与圆锥曲线的关系,轨迹方程的求解,属于中档题.

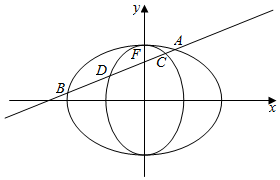 如图的椭圆C1,C2的离心率相等,中心均为坐标原点,焦点分别在x轴和y轴上,且两椭圆都过点(0,$\sqrt{2}$),设点F是椭圆C2的上焦点,过点F的动直线l交椭圆C1于A,B两点,交椭圆C2于C,D两点,当直线l经过椭圆C1的左焦点时,$\frac{|AB|}{|CD|}$=$\frac{5\sqrt{2}}{4}$.
如图的椭圆C1,C2的离心率相等,中心均为坐标原点,焦点分别在x轴和y轴上,且两椭圆都过点(0,$\sqrt{2}$),设点F是椭圆C2的上焦点,过点F的动直线l交椭圆C1于A,B两点,交椭圆C2于C,D两点,当直线l经过椭圆C1的左焦点时,$\frac{|AB|}{|CD|}$=$\frac{5\sqrt{2}}{4}$.