题目内容
8.设实数$α∈\left\{{-2,-1,\frac{1}{2},1,3}\right\}$,如果函数y=xα是定义域为R的奇函数,则α的值的集合为{1,3}.分析 讨论α的取值,得出函数y=xα是定义域R上的奇函数时α的取值范围.
解答 解:∵实数α∈{-2,-1,$\frac{1}{2}$,1,3},
∴当α=-1时,函数y=x-1是定义域(-∞,0)∪(0,+∞)上的奇函数,不满足题意;
当α=1时,函数y=x是定义域R上的奇函数,满足题意;
当α=3时,函数y=x3是定义域R上的奇函数,满足题意;
∴α的取值集合为{1,3}.
点评 本题考查了幂函数的定义与单调性质的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知抛物线C:y2=8x,过点(0,-2)且斜率为k的直线l与抛物线C交于不同的两点A,B.
(Ⅰ)求抛物线C的准线方程;
(Ⅱ)求实数k的取值范围;
(Ⅲ)若线段AB中点的横坐标为2,求AB的长度.
(Ⅰ)求抛物线C的准线方程;
(Ⅱ)求实数k的取值范围;
(Ⅲ)若线段AB中点的横坐标为2,求AB的长度.
20.已知a=tan1,b=tan2,c=tan3,则a,b,c的大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | c>a>b |
18.某民营企业生产甲、乙两种产品,根据以往经验和市场调查,甲产品的利润与投入资金成正比,乙产品的利润与投入资金的算术平方根成正比,已知甲、乙产品分别投入资金4万元时,所获得利润(万元)情况如下:
该企业计划投入资金10万元生产甲、乙两种产品,那么可获得的最大利润(万元)是( )
| 投入资金 | 甲产品利润 | 乙产品利润 |
| 4 | 1 | 2.5 |
| A. | $\frac{9}{2}$ | B. | $\frac{65}{16}$ | C. | $\frac{35}{8}$ | D. | $\frac{17}{4}$ |
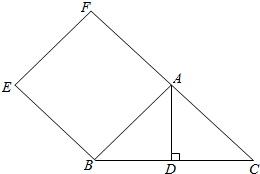 如图,已知正方形ABEF的面积为10,以AB为直角边所作的等腰直角角形ABC的斜边BC=2$\sqrt{5}$,求BC边上的高AD的长度.
如图,已知正方形ABEF的面积为10,以AB为直角边所作的等腰直角角形ABC的斜边BC=2$\sqrt{5}$,求BC边上的高AD的长度. 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点在抛物线y2=4$\sqrt{2}$x的准线上,离心率为$\frac{\sqrt{6}}{3}$,若不过椭圆E上顶点A的动直线l与椭圆E交于P、Q两点,且$\overrightarrow{AP}$•$\overrightarrow{AQ}$=0.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点在抛物线y2=4$\sqrt{2}$x的准线上,离心率为$\frac{\sqrt{6}}{3}$,若不过椭圆E上顶点A的动直线l与椭圆E交于P、Q两点,且$\overrightarrow{AP}$•$\overrightarrow{AQ}$=0.