题目内容
18．三棱锥P-ABC中，PA⊥底面ABC，PA=3，底面ABC是边长为2的正三角形，则三棱锥P-ABC的体积等于（ ）| A． | 3$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | 2$\sqrt{3}$ | D． | 4$\sqrt{3}$ |
分析 由题意求出底面面积，然后求出三棱锥的体积．
解答 解：三棱锥P-ABC中，PA⊥底面ABC，PA=3，底面ABC是边长为2的正三角形，所以底面面积为：$\sqrt{3}$；
三棱锥的体积为：$\frac{1}{3}$×$\sqrt{3}$×3=$\sqrt{3}$
故选：B．
点评 本题是基础题，考查三棱锥的体积的计算，注意三棱锥的特征是解题的关键．
练习册系列答案
相关题目
6．命题p：?a∈（-∞，-$\frac{1}{4}$]，使得函数f（x）=|2x+$\frac{a}{{2}^{x}}$|在[-$\frac{1}{2}$，3]上单调递增；命题q：?a∈[2，+∞），直线2x+y=0与双曲线$\frac{{y}^{2}}{{a}^{2}}$-x2=1（a＞0）相交．则下列命题中正确的是（ ）
| A． | ￢p | B． | p∧q | C． | （￢p）∨q | D． | p∧（￢q） |
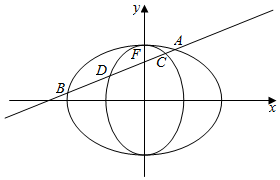如图的椭圆C1，C2的离心率相等，中心均为坐标原点，焦点分别在x轴和y轴上，且两椭圆都过点（0，$\sqrt{2}$），设点F是椭圆C2的上焦点，过点F的动直线l交椭圆C1于A，B两点，交椭圆C2于C，D两点，当直线l经过椭圆C1的左焦点时，$\frac{|AB|}{|CD|}$=$\frac{5\sqrt{2}}{4}$．
8．若“?x∈[$\frac{π}{3}$，$\frac{2π}{3}$]，cosx≤m”是真命题，则实数m的最小值为（ ）
| A． | -$\frac{1}{2}$ | B． | -$\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |