题目内容
11.已知数列{an}(n=1,2,3,…),⊙C1:x2+y2-2anx+2an+1y-2=0和⊙C2:x2+y2+2x+2y-2=0.若⊙C1和⊙C2交于A、B两点,且这两点平分⊙C2的周长(1)求证数列{an}是等差数列;
(2)若a1=1,则当⊙C1面积最小时,求出⊙C1的方程.
分析 (1)⊙C1和⊙C2的方程相减可得直线AB的方程:(1+an)x+(1-an+1)y=0.由于⊙C1和⊙C2交于A、B两点,且这两点平分⊙C2的周长,可得AB经过⊙C2的圆心(-1,-1),可得1+an+1-an+1=0,即可证明.
(2)当a1=1时,an=2n-1.⊙C1:x2+y2-2anx+2an+1y-2=0配方变为:$(x-{a}_{n})^{2}$+$(y+{a}_{n+1})^{2}$=${a}_{n}^{2}+{a}_{n+1}^{2}$+2.半径R满足:R2=${a}_{n}^{2}+{a}_{n+1}^{2}$+2=(2n-1)2+(2n+1)2+2=8n2+4≥12,即可得出.
解答 (1)证明:⊙C1:x2+y2-2anx+2an+1y-2=0和⊙C2:x2+y2+2x+2y-2=0相减可得直线AB的方程:(1+an)x+(1-an+1)y=0.
∵⊙C1和⊙C2交于A、B两点,且这两点平分⊙C2的周长,
∴AB经过⊙C2的圆心(-1,-1),
∴1+an+1-an+1=0,即an+1-an=2,
∴数列{an}是公差为2的等差数列.
(2)解:当a1=1时,an=1+2(n-1)=2n-1.
⊙C1:x2+y2-2anx+2an+1y-2=0配方变为:$(x-{a}_{n})^{2}$+$(y+{a}_{n+1})^{2}$=${a}_{n}^{2}+{a}_{n+1}^{2}$+2.
半径R满足:R2=${a}_{n}^{2}+{a}_{n+1}^{2}$+2=(2n-1)2+(2n+1)2+2=8n2+4≥12,当n=1时q取等号,
此时⊙C1面积最小,⊙C1的方程为:(x-1)2+(y+3)2=12.
点评 本题考查了递推关系、等差数列的通项公式、圆的性质,考查了推理能力与计算能力,属于中档题.

| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | c>a>b |
| A. | .充分不必要条件 | B. | .必要不充分条件 | ||
| C. | .充要条件 | D. | 既非充分又非必要条件 |
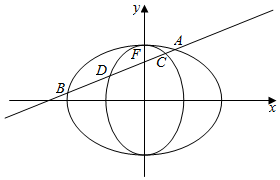 如图的椭圆C1,C2的离心率相等,中心均为坐标原点,焦点分别在x轴和y轴上,且两椭圆都过点(0,$\sqrt{2}$),设点F是椭圆C2的上焦点,过点F的动直线l交椭圆C1于A,B两点,交椭圆C2于C,D两点,当直线l经过椭圆C1的左焦点时,$\frac{|AB|}{|CD|}$=$\frac{5\sqrt{2}}{4}$.
如图的椭圆C1,C2的离心率相等,中心均为坐标原点,焦点分别在x轴和y轴上,且两椭圆都过点(0,$\sqrt{2}$),设点F是椭圆C2的上焦点,过点F的动直线l交椭圆C1于A,B两点,交椭圆C2于C,D两点,当直线l经过椭圆C1的左焦点时,$\frac{|AB|}{|CD|}$=$\frac{5\sqrt{2}}{4}$. 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点在抛物线y2=4$\sqrt{2}$x的准线上,离心率为$\frac{\sqrt{6}}{3}$,若不过椭圆E上顶点A的动直线l与椭圆E交于P、Q两点,且$\overrightarrow{AP}$•$\overrightarrow{AQ}$=0.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点在抛物线y2=4$\sqrt{2}$x的准线上,离心率为$\frac{\sqrt{6}}{3}$,若不过椭圆E上顶点A的动直线l与椭圆E交于P、Q两点,且$\overrightarrow{AP}$•$\overrightarrow{AQ}$=0.