题目内容

13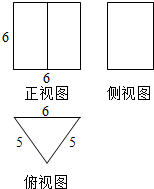．某几何体的三视图如图所示，其中正视图是边长为6的正方形，俯视图是腰长为5，底边长为6的等腰三角形，则该几何体的体积是72，表面积是120．

分析 由三视图可知几何体是一个三棱柱，此三棱柱的高为6，底面正三角形的高为4，利用表面积公式和体积公式得到结果．

解答 解：由三视图图可知此三棱柱的高为6，底面正三角形的高为4，
可求得底面面积为：$\frac{1}{2}×6×4$=12．
∴V=S•h=6×12=72
S表面=2S底+S侧面=2×12+6×（6+5+5）=120

点评 本题考查有三视图求几何体的体积和表面积，解题时要注意看清各个位置的长度，不要在数字运算上出错．

练习册系列答案
相关题目
3．设命题q：对任意实数x，不等式x2-2x+m≥0恒成立；命题q：方程$\frac{x^2}{m-3}-\frac{y^2}{m}=1$表示焦点在x轴上的双曲线．
（1）若命题q为真命题，求实数m的取值范围；
（ 2）若命题：“p∨q”为真命题，且“p∧q”为假命题，求实数m的取值范围．
4．给出以下命题：
①方程4x2-8x+3=0的两个根可分别作为椭圆与双曲线的离心率；
②若向量$\overrightarrow{a}$=（m，-2，3）与$\overrightarrow{b}$=（5，m2，1）的夹角为锐角，则-$\frac{1}{2}$＜m＜3；
③在正项等差数列{an}中，$\frac{a_3}{a_2+a_9}$+$\frac{a_8}{a_5+a_6}$=1；
④当x＞0时，函数f（x）=x2+$\frac{1}{x^2}$-8x-$\frac{8}{x}$+22的最小值是4．
其中正确命题的序号是①②③④．
1．若位于x轴上方、且到点A（-2，0）和B（2，0）的距离的平方和为18的点的轨迹为曲线C，点P的坐标为（a，b），则“$b=\sqrt{5-{a^2}}$”是“点P在曲线C上”的（　　）
A．.充分不必要条件B．.必要不充分条件
C．.充要条件D．既非充分又非必要条件
8．若“?x∈[$\frac{π}{3}$，$\frac{2π}{3}$]，cosx≤m”是真命题，则实数m的最小值为（　　）
A．-$\frac{1}{2}$B．-$\frac{\sqrt{3}}{2}$C．$\frac{1}{2}$D．$\frac{\sqrt{3}}{2}$
18．某民营企业生产甲、乙两种产品，根据以往经验和市场调查，甲产品的利润与投入资金成正比，乙产品的利润与投入资金的算术平方根成正比，已知甲、乙产品分别投入资金4万元时，所获得利润（万元）情况如下：
投入资金甲产品利润乙产品利润
412.5
该企业计划投入资金10万元生产甲、乙两种产品，那么可获得的最大利润（万元）是（　　）
A．$\frac{9}{2}$B．$\frac{65}{16}$C．$\frac{35}{8}$D．$\frac{17}{4}$
5．设直线l1：x+my+6=0和l2：（m-2）x+3y+2m=0，当m=-1时，l1∥l2，当m=$\frac{1}{2}$时，l1⊥l2．
2．已知f（x）为偶函数，且当x≥0时，f（x）=x（1+x），则满足f（x）≤2的x的取值范围是[-1，1]．
3．已知数列{an}满足${a_1}=6，{a_{n+1}}=4-\frac{4}{a_n}（n$为正整数）．
（Ⅰ）求证：数列$\{\frac{{{a_n}+2}}{{{a_n}-2}}\}$为等差数列；
（Ⅱ）若${b_n}=\frac{a_n}{{{{（2n+1）}^2}}}$，求数列{bn}的前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网