题目内容
若函数f(x)=2sin(3x-
),有下列结论:
①函数f(x)的图象关于点(
,0)对称;
②函数f(x)的图象关于直线x=
π对称;
③在x∈[
,
π]为单调增函数.
则上述结论题正确的是 .(填相应结论对应的序号)
| 3π |
| 4 |
①函数f(x)的图象关于点(
| 7π |
| 12 |
②函数f(x)的图象关于直线x=
| 5 |
| 12 |
③在x∈[
| π |
| 12 |
| 5 |
| 12 |
则上述结论题正确的是
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:根据三角函数的图象和性质分别进行判断即可得到结论.
解答:
解:①f(
)=2sin(3×
-
)=2sinπ=0,则函数图象关于点(
,0)对称,故①正确,
②f(
π)=2sin(3×
π-
)=2sin
=2,则图象关于直线x=
π对称,故②正确,
③当x∈[
,
π],3x-
∈[-
,
],此时函数单调递增,故③正确,
故答案为:①②③.
| 7π |
| 12 |
| 7π |
| 12 |
| 3π |
| 4 |
| 7π |
| 12 |
②f(
| 5 |
| 12 |
| 5 |
| 12 |
| 3π |
| 4 |
| π |
| 2 |
| 5 |
| 12 |
③当x∈[
| π |
| 12 |
| 5 |
| 12 |
| 3π |
| 4 |
| π |
| 2 |
| π |
| 2 |
故答案为:①②③.
点评:本题主要考查与三角函数命题有关的真假判断,根据三角函数的图象和性质是解决本题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
直线y=x-1与双曲线x2-
=1(b>0)有两个不同的交点,则此双曲线离心率的范围是( )
| y2 |
| b2 |
A、(1,
| ||||
B、(
| ||||
| C、(1,+∞) | ||||
D、(1,
|
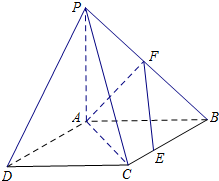 如图,四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点.
如图,四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点.