题目内容
已知向量
=(sinωx-cosωx,sinωx),
=(sinωx+cosωx,
cosωx).设函数f(x)=
•
+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
,1).
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点(
,0),求函数f(x)在区间[0,
]上的取值范围.
| a |
| b |
| 3 |
| a |
| b |
| 1 |
| 2 |
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点(
| π |
| 5 |
| π |
| 2 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:三角函数的求值
分析:(1)由条件利用两个向量的数量积公式、三角恒等变换求得f(x)=
•
+λ=2sin(2ωx-
)+λ,再根据函数f(x)的图象关于直线x=π对称,可得2ω•π-
=kπ+
,k∈z,结合ω∈(
,1),可得ω 的值.
(2)由y=f(x)的图象经过点(
,0),求得λ的值,可得f(x)=2sin(
x-
)-1.由 0≤x≤
,利用正弦函数的定义域和值域求得函数f(x)在区间[0,
]上的取值范围.
| a |
| b |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| 1 |
| 2 |
(2)由y=f(x)的图象经过点(
| π |
| 5 |
| 5 |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
解答:
解:(1)∵f(x)=
•
+λ=sin2ωx-cos2ωx+2
sinωxcosωx+λ
=-cos2ωx+
sin2ωx+λ=2sin(2ωx-
)+λ,
再根据函数f(x)的图象关于直线x=π对称,可得sin(2ωx-
)=±1,
2ω•π-
=kπ+
,k∈z,即ω=
+
.
结合ω∈(
,1),可得ω=
.
(2)由y=f(x)的图象经过点(
,0),得 f(
)=0.
即λ=-2sin(
×
-
)=-2sin
=-1,故 f(x)=2sin(
x-
)-1.
由 0≤x≤
,有-
≤
x-
≤
.
∴-
≤2sin(
x-
)≤1,得-2≤f(x)≤1.
所以,函数f(x)在区间[0,
]上的取值范围为[-2,1].
| a |
| b |
| 3 |
=-cos2ωx+
| 3 |
| π |
| 6 |
再根据函数f(x)的图象关于直线x=π对称,可得sin(2ωx-
| π |
| 6 |
2ω•π-
| π |
| 6 |
| π |
| 2 |
| k |
| 2 |
| 1 |
| 3 |
结合ω∈(
| 1 |
| 2 |
| 5 |
| 6 |
(2)由y=f(x)的图象经过点(
| π |
| 5 |
| π |
| 5 |
即λ=-2sin(
| 5 |
| 6 |
| 2π |
| 5 |
| π |
| 6 |
| π |
| 6 |
| 5 |
| 3 |
| π |
| 6 |
由 0≤x≤
| π |
| 2 |
| π |
| 6 |
| 5 |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
∴-
| 1 |
| 2 |
| 5 |
| 3 |
| π |
| 6 |
所以,函数f(x)在区间[0,
| π |
| 2 |
点评:本题主要考查两个向量的数量积公式,三角恒等变换,正弦函数图象的对称性,正弦函数的定义域和值域,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
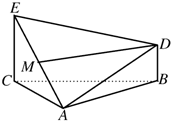 如图所示,已知△ABC是等边三角形,EC⊥平面ABC,BD⊥平面ABC,且EC、DB在平面ABC的同侧,M为EA的中点,CE=2BD.
如图所示,已知△ABC是等边三角形,EC⊥平面ABC,BD⊥平面ABC,且EC、DB在平面ABC的同侧,M为EA的中点,CE=2BD.