题目内容
某同学参加政治、历史、生物、地理四门学科的学业水平测试,假设该同学历史学科测试成绩为A的概率为
,其余三门学科测试成绩为A的概率均为
,且四门学科测试成绩是否为A相互独立.
(1)求该同学恰有两门学科测试成绩为A的概率;
(2)设四门学科中测试成绩为A的门数为ξ,求ξ的分布列及数学期望.
| 4 |
| 5 |
| 1 |
| 2 |
(1)求该同学恰有两门学科测试成绩为A的概率;
(2)设四门学科中测试成绩为A的门数为ξ,求ξ的分布列及数学期望.
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:(1)设事件Ai(i=1,2,3,4)分别表示“该同学政治、历史、生物、地理”四门学科测试成绩为A”,则P(A1)=
,P(A2)=P(A3)=P(A4)=
,由此能求出该同学恰有两门学科测试成绩为A的概率.
(2)随机变量ξ的可能取值是0,1,2,3,4,分别求出相应的概率,由此能求出ξ的分布列及数学期望.
| 4 |
| 5 |
| 1 |
| 2 |
(2)随机变量ξ的可能取值是0,1,2,3,4,分别求出相应的概率,由此能求出ξ的分布列及数学期望.
解答:
解:(1)设事件Ai(i=1,2,3,4)分别表示
“该同学政治、历史、生物、地理”四门学科测试成绩为A”,
则P(A1)=
,P(A2)=P(A3)=P(A4)=
,
该同学恰有两门学科测试成绩为A的概率是:
P=P(A1A2
)+P(A1A3
)+P(A1A4
)
+P(A2A3
)+P(A2A4
)+P(A3A4
)
=
×
×(1-
)2
×(
)2×(1-
)×(1-
)=
.
∴该同学恰有两门学科测试成绩为A的概率是
.
(2)随机变量ξ的可能取值是0,1,2,3,4,
P(ξ=0)=
×(
)3=
,
P(ξ=1)=
×(
)3+
×(
)3×
=
,
P(ξ=2)═
×
×(1-
)2
×(
)2×(1-
)×(1-
)=
,
P(ξ=3)=
×(
)3
(
)3×
=
,
P(ξ=4)=
×(
)3=
,
∴ξ的分布列为:
∴Eξ=0×
+1×
+2×
+3×
+4×
=
.
“该同学政治、历史、生物、地理”四门学科测试成绩为A”,
则P(A1)=
| 4 |
| 5 |
| 1 |
| 2 |
该同学恰有两门学科测试成绩为A的概率是:
P=P(A1A2
. |
| A3 |
. |
| A4 |
. |
| A2 |
. |
| A4 |
. |
| A2 |
. |
| A3 |
+P(A2A3
. |
| A1 |
. |
| A4 |
. |
| A1 |
. |
| A3 |
. |
| A1 |
. |
| A2 |
=
| 4 |
| 5 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| +C | 2 3 |
| 1 |
| 2 |
| 4 |
| 5 |
| 1 |
| 2 |
| 3 |
| 8 |
∴该同学恰有两门学科测试成绩为A的概率是
| 3 |
| 8 |
(2)随机变量ξ的可能取值是0,1,2,3,4,
P(ξ=0)=
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 40 |
P(ξ=1)=
| 4 |
| 5 |
| 1 |
| 2 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 5 |
| 7 |
| 40 |
P(ξ=2)═
| 4 |
| 5 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| +C | 2 3 |
| 1 |
| 2 |
| 4 |
| 5 |
| 1 |
| 2 |
| 3 |
| 8 |
P(ξ=3)=
| 1 |
| 5 |
| 1 |
| 2 |
| C | 2 3 |
| 1 |
| 2 |
| 4 |
| 5 |
| 13 |
| 40 |
P(ξ=4)=
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 10 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 40 |
| 7 |
| 40 |
| 3 |
| 8 |
| 13 |
| 40 |
| 1 |
| 10 |
| 23 |
| 10 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
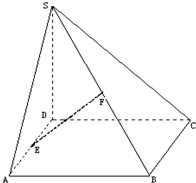 已知:如图,四棱锥S-ABCD底面为平行四边形,E、F分别为边AD、SB中点,
已知:如图,四棱锥S-ABCD底面为平行四边形,E、F分别为边AD、SB中点, 如图为函数y=Asin(ωx+φ)(A,ω>0,|φ|<π)图象的一段.
如图为函数y=Asin(ωx+φ)(A,ω>0,|φ|<π)图象的一段.