题目内容
设命题p:函数f(x)=x2-ax-1在区间[-1,1]上单调递减;命题q:函数y=ln(x2+ax+1)的定义域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:首先,判断命题p和命题q的真假,然后,结合条件:命题p或q为真命题,p且q为假命题,得到两个命题中,必有一个为假命题,一个为真命题,最后,求解得到结论.
解答:
解:命题p:函数f(x)=x2-ax-1在区间[-1,1]上单调递减,
∴
≥1,
∴a≥2,
命题q:函数y=ln(x2+ax+1)的定义域是R,
∴x2+ax+1>0,
∴△=a2-4<0,
解得:-2<a<2;
∵命题p或q为真命题,p且q为假命题,
∴两个命题中,必有一个为假命题,一个为真命题,
当命题p为真,命题q为假时,有
,
解得:a≥2,即a∈[2,+∞);
当命题q为真,命题p为假时,有
,
解得:-2<a<2;
∴a的取值范围(-2,+∞).
∴
| a |
| 2 |
∴a≥2,
命题q:函数y=ln(x2+ax+1)的定义域是R,
∴x2+ax+1>0,
∴△=a2-4<0,
解得:-2<a<2;
∵命题p或q为真命题,p且q为假命题,
∴两个命题中,必有一个为假命题,一个为真命题,
当命题p为真,命题q为假时,有
|
解得:a≥2,即a∈[2,+∞);
当命题q为真,命题p为假时,有
|
解得:-2<a<2;
∴a的取值范围(-2,+∞).
点评:本题重点考查了简单命题的真假判断,复合命题的真值表应用,注意“且”“或”的含义,属于中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
已知f(x)=
是(-∞,+∞)上的减函数,那么a的取值范围是( )
|
| A、(-∞,1] | ||||
B、[
| ||||
| C、[0,1] | ||||
D、(
|
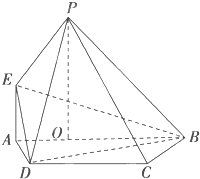 如图,PO⊥平面ABCD,点O在AB上,EA∥PO,四边形ABCD为直角梯形,BC⊥AB,BC=CD=BO=PO,EA=AO=
如图,PO⊥平面ABCD,点O在AB上,EA∥PO,四边形ABCD为直角梯形,BC⊥AB,BC=CD=BO=PO,EA=AO=