题目内容
6.在△ABC中,角A,B,C对边分别为a,b,c.若A=$\frac{π}{6}$,a=3,b=4,则$\frac{a+b}{sinA+sinB}$=( )| A. | $3\sqrt{3}$ | B. | $6\sqrt{3}$ | C. | 6 | D. | 18 |
分析 由正弦定理,$\frac{a}{sinA}=\frac{b}{sinB}$,求得sinB=$\frac{2}{3}$,代入$\frac{a+b}{sinA+sinB}$的值即可.
解答 解:由正弦定理可知,$\frac{a}{sinA}=\frac{b}{sinB}$,
∴sinB=$\frac{bsinA}{a}$=$\frac{4×\frac{1}{2}}{3}$=$\frac{2}{3}$,
∴$\frac{a+b}{sinA+sinB}$=$\frac{3+4}{\frac{1}{2}+\frac{2}{3}}$=6,
故答案选:C.
点评 本题考查正弦定理,过程简单,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知函数f(x)是在定义域内最小正周期为π的奇函数,且在区间(0,$\frac{π}{2}$)是减函数,那么函数f(x)可能是( )
| A. | f(x)=sin2x | B. | f(x)=2tan$\frac{1}{2}$x | C. | f(x)=-tanx | D. | f(x)=sin($\frac{π}{2}$+2x) |
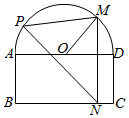 如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=2,BC=4,现要将此铁皮剪出一个△PMN,其中边MN⊥BC,点P在曲线MAB上运动.
如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=2,BC=4,现要将此铁皮剪出一个△PMN,其中边MN⊥BC,点P在曲线MAB上运动. 如图是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+\frac{1}{10}$的值一个程序框图,其中判断框内可填入的条件是k>5.(请写出关于k的一个不等式)
如图是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+\frac{1}{10}$的值一个程序框图,其中判断框内可填入的条件是k>5.(请写出关于k的一个不等式)