题目内容
1.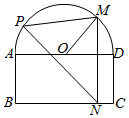 如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=2,BC=4,现要将此铁皮剪出一个△PMN,其中边MN⊥BC,点P在曲线MAB上运动.
如图,一个半圆和长方形组成的铁皮,长方形的边AD为半圆的直径,O为半圆的圆心,AB=2,BC=4,现要将此铁皮剪出一个△PMN,其中边MN⊥BC,点P在曲线MAB上运动.(1)设∠MOD=30°,若PM=PN,求△PMN的面积;
(2)求剪下的铁皮△PMN面积的最大值.
分析 (1)设MN交AD交于Q点由∠MOD=30°,利用锐角三角函数可求MQ,OQ,进而可求MN,AQ,代入S△PMN=$\frac{1}{2}$MN•AQ可求;
(2)设∠MOQ=θ,由θ∈[0,$\frac{π}{2}$],结合锐角三角函数的定义可求MQ=sinθ,OQ=cosθ,代入三角形的面积公式S△PMN=$\frac{1}{2}$MN•AQ=$\frac{1}{2}$(1+sinθ)(1+cosθ)展开利用换元法,转化为二次函数的最值求解.
解答 解:(1)设MN交AD交于Q点,
∵PM=PN,
∴点P在线段AB上,
∵∠MQD=30°,
∴MQ=1,OQ=$\sqrt{3}$
∴S△PMN=$\frac{1}{2}$MN•AQ=$\frac{1}{2}$×3×(2+$\sqrt{3}$)=$\frac{{6+3\sqrt{3}}}{2}$….…(7分)
(2)设∠MOD=θ$({θ∈[{0,\frac{π}{2}}]})$,则 MQ=2sinθ,OQ=2cosθ.
设P到MN的距离为h,则h≤|AQ|=2+2cosθ,
∴S△PMN=$\frac{1}{2}$MN•h≤$\frac{1}{2}$(2+2sinθ)(2+2cosθ)=2 (1+sinθcosθ+sinθ+cosθ)
令sinθ+cosθ=t∈$[{1,\sqrt{2}}]$,则S△PMN=2 (1+$\frac{{{t^2}-1}}{2}$+t)=(t+1)2
当t=$\sqrt{2}$即θ=$\frac{π}{4}$,且P在线段AB上时,S△PMN取得最大值,最大值为$3+2\sqrt{2}$.…(15分)
点评 本题主要考查了三角函数的定义的应用及利用三角函数求解函数的最值,换元法的应用是求解的关键,属于中档题.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案| A. | bn>cn | B. | bn<cn | C. | bn≥cn | D. | bn≤cn |
| A. | $3\sqrt{3}$ | B. | $6\sqrt{3}$ | C. | 6 | D. | 18 |
| A. | $\frac{14π}{3}$ | B. | $-\frac{14π}{3}$ | C. | $\frac{7π}{18}$ | D. | $-\frac{7π}{18}$ |