题目内容
设(2x+1)5+(x-2)4=a0+a1x+a2x2+a3x3+a4x4+a5x5,则a2= .
考点:二项式系数的性质
专题:二项式定理
分析:由题意可得,a2就是x2的系数,再根据二项式的展开式的通项公式可得x2的系数为
•22+
•22,计算求得结果.
| C | 3 5 |
| C | 2 4 |
解答:
解:由题意可得,a2就是x2的系数,
再根据二项式的展开式的通项公式可得x2的系数为
•22+
•22=40+24=64,
故答案为:64.
再根据二项式的展开式的通项公式可得x2的系数为
| C | 3 5 |
| C | 2 4 |
故答案为:64.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
执行如图所示的程序框图,若输入n的值为7,则输出s的值是( )
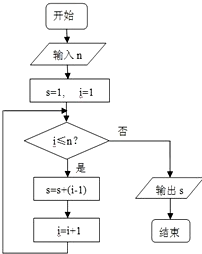

| A、10 | B、16 | C、22 | D、17 |
“m=1”是“复数z=(1+mi)(1+i)(m∈R,i为虚数单位)为纯虚数”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
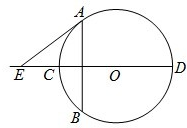 如图,AB是圆O的弦,CD是AB的垂直平分线,切线AE与DC的延长线相交于E.若AB=24,AE=20,则圆O的半径R=
如图,AB是圆O的弦,CD是AB的垂直平分线,切线AE与DC的延长线相交于E.若AB=24,AE=20,则圆O的半径R=