题目内容
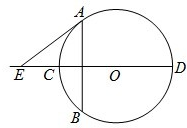如图，AB是圆O的弦，CD是AB的垂直平分线，切线AE与DC的延长线相交于E．若AB=24，AE=20，则圆O的半径R=考点：与圆有关的比例线段
专题：直线与圆
分析：设AB∩CD=F，连结OA，由已知条件推导出△AFE∽△OAE，从而得到
=
，由此根据题设条件能求出圆O的半径R．
| AF |
| OA |
| EF |
| AE |
解答：
解：设AB∩CD=F，连结OA，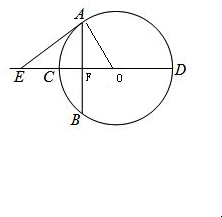
∵AB是圆O的弦，CD是AB的垂直平分线，
切线AE与DC的延长线相交于E，
∴∠AFE=∠OAE=90°，∠E=∠E，
∴△AFE∽△OAE，
∴
=
，
∵AB=24，AE=20，
∴AF=
AB=12，EF=
=16，
∴OA=
=
=15．
故答案为：15．
∵AB是圆O的弦，CD是AB的垂直平分线，
切线AE与DC的延长线相交于E，
∴∠AFE=∠OAE=90°，∠E=∠E，
∴△AFE∽△OAE，
∴
| AF |
| OA |
| EF |
| AE |
∵AB=24，AE=20，
∴AF=
| 1 |
| 2 |
| 202-122 |
∴OA=
| AE•AF |
| EF |
| 20•12 |
| 16 |
故答案为：15．
点评：本题考查圆的半径长的求法，是中档题，解题时要注意垂径定理、切线性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
如图，在圆的内接四边形ABCD中，∠ABC=90°，∠ABD=30°，∠BDC=45°，AD=1，则BC=已知椭圆C：
+
=1（a＞b＞0）的左焦点为F，右顶点为A，其长轴长是焦距的4倍，且抛物线y2=6x的焦点平分线段AF，则椭圆C的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|