题目内容
证明：card（A∪B∪C）=card（A）+card（B）+card（C）-card（A∩B）-card（A∩C）-card（B∩C）+card（A∩B∩C）考点：集合中元素个数的最值
专题：证明题,集合
分析：计数容斥原理，“容”就是加进来，“斥”就是把多加了的减出去，即可证明结论．
解答：
证明：card（A∪B∪C）=card[（A∪B）∪C]=card（A∪B）+card（C）-card[（A∪B）∩C]，
而card（A∪B）=card（A）+card（B）-card（A∩B），
card[（A∪B）∩C]=card[（A∩C）∪（B∩C）]=card（A∩C）+card（B∩C）-card[（A∩C）∩（B∩C）]，
card[（A∩C）∩（B∩C）]=card（A∩B∩C），
所以card（A∪B∪C）=card（A）+card（B）+card（C）-card（A∩B）-card（A∩C）-card（B∩C）+card（A∩B∩C）．
而card（A∪B）=card（A）+card（B）-card（A∩B），
card[（A∪B）∩C]=card[（A∩C）∪（B∩C）]=card（A∩C）+card（B∩C）-card[（A∩C）∩（B∩C）]，
card[（A∩C）∩（B∩C）]=card（A∩B∩C），
所以card（A∪B∪C）=card（A）+card（B）+card（C）-card（A∩B）-card（A∩C）-card（B∩C）+card（A∩B∩C）．
点评：本题考查计数容斥原理，“容”就是加进来，“斥”就是把多加了的减出去，属于基础题．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
已知双曲线
-
=1（a，b＞0）抛物线y2=4x共焦点，双曲线与抛物线的一公共点到抛物线准线的距离为2，双曲线的离心率为e，则2e-b2的值是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、2
| ||
C、4-2
| ||
| D、4 |
已知正三角形ABC的顶点A（
，1），B（3
，1），顶点C在第一象限，若点M（x，y）在△ABC的内部或边界，则z=
•
取最大值时，3x2+y2有（ ）
| 3 |
| 3 |
| OA |
| OM |
| A、定值52 | B、定值82 |
| C、最小值52 | D、最小值50 |
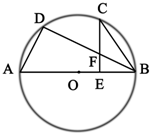如图：AB是⊙O的直径，C是弧BD的中点，CE⊥AB，垂足为E，BD交CE于点F．